Pascal's triangle
When performing computations in problems involving probability and statistics, it’s often helpful to have the binomial coefficients found in Pascal’s triangle. These numbers are the results of finding combinations of n things taken k at a time. For quick reference, the first ten rows of the triangle are shown.

Binomial distributions
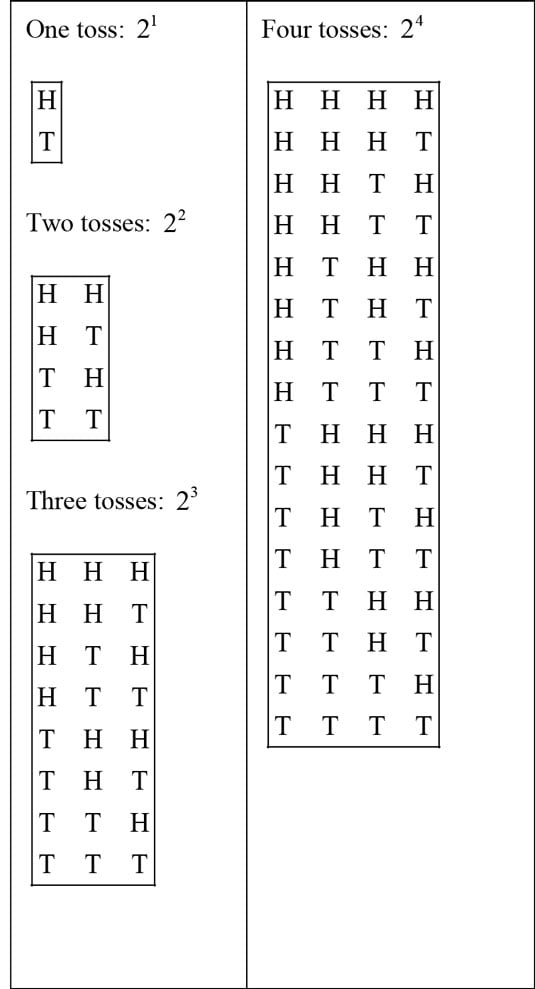
A common situation when doing probability problems is having to determine the patterns of heads-and-tails, boys-and-girls, true-or-false arrangements. When there are two choices, there are 2n ways that they can occur. The following refer to Heads-or-Tails in a coin-flipping situation but can be adapted to any binomial arrangement.
Matrix notation
Matrices are rectangular arrangements of elements. The dimension of a matrix is given with m × n where m is the number of rows and n is the number of columns. The elements are identified with subscripts giving the row, j, and column, k, shown as ajk for the elements of a matrix A.
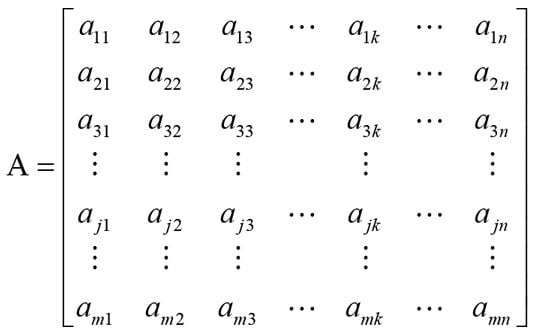
When multiplying the matrices, the number of rows in the first matrix has to equal the number of columns in the second. Given matrices A and B where A has dimension 2 × 3 and B has the dimension3 × 2, the resulting matrices are found as follows:
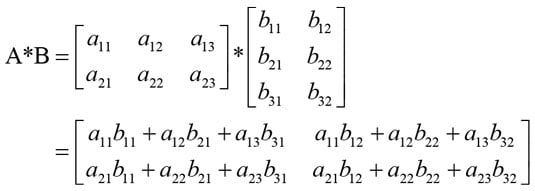
Factorial
The factorial operation says to multiply the designated number by every positive integer smaller than that number.
n! = n (n – 1) (n – 2) 3 2 1
When using the operation in the formulas for the number of permutations or combinations of n things taken k at a time, factorial values need to be inserted into the numerator and denominator of the fraction. The first sixteen factorial values are given here. And, by definition, 0! = 1.
| n | n! | n | n! |
| 1 | 1 | 9 | 362,880 |
| 2 | 2 | 10 | 3,628,800 |
| 3 | 6 | 11 | 39,916,800 |
| 4 | 24 | 12 | 479,001,600 |
| 5 | 120 | 13 | 6,227,020,800 |
| 6 | 720 | 14 | 87,178,291,200 |
| 7 | 5,040 | 15 | 1,307,674,368,000 |
| 8 | 40,320 | 16 | 20,922,789,888,000 |

