Two types of connectives that you often see in a compound statement are conjunctions and disjunctions, represented by ∧ and ∨, respectively.
It’s important to know the difference between these two connectives.
Identifying a conjunction
The conjunction, p ∧ q, puts the word and between two statements to create a compound statement.Consider the following statements:
(1) Chicago is a city in Illinois.
(2) Red is a color in the American flag.
(3) 7 + 3 = 11.
(4) San Francisco is a city in Florida.
Statements (1) and (2) are true, and Statements (3) and (4) are false.
Next, you construct a truth table for the conjunction p ^ q.
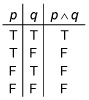
Referring to the first line of Ts and Fs in the table, when both statements are true, their conjunction p ^ q is true. For example, using Statements (1) and (2), the conjunction reads: “Chicago is a city in Illinois, and red is a color in the American flag.”
The second line of Ts and Fs says that when the first statement is true and the second is false, their conjunction p ^ q is false. Using Statements (1) and (3), the conjunction reads: “Chicago is a city in Illinois, and .”
In the third line, when the first statement is false and the second statement is true, their conjunction p ^ q is false. Using Statements (4) and (2), the conjunction reads: “San Francisco is a city in Florida, and red is a color in the American flag.”
And, finally, when both statements are false, their conjunction is false. Using Statements (3) and (4), the conjunction reads: “7 + 3 = 11, and San Francisco is a city in Florida.”
Basically, what you see here is that for a conjunction to be true, both of the component statements have to be true.
Identifying a disjunction
The disjunction, p ∨ q, uses the word or to create a compound statement.The truth table for the disjunction is shown here:
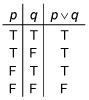
For a disjunction to be true, only one of the component statements needs to be true. Consider the following compound statements representing the four rows.
Both are true; the compound statement is true.
TF: “It rains in Hawaii, or all cows have seven legs.” The first statement is true, so the compound statement is true.
The second statement is true, so the compound statement is true.
FF: “All cows have seven legs, or pigs can fly.” Both statements are false, so the compound statement is false.

