The shell method is useful when you’re measuring a volume of revolution around the y-axis. For example, suppose that you want to measure the volume of the solid shown in this figure.
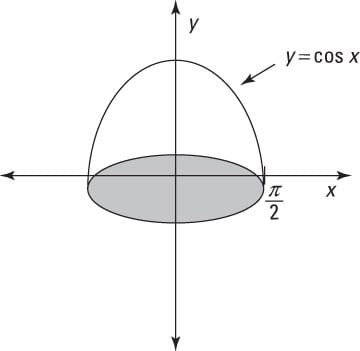
Here’s how the shell method can give you a solution:
Find an expression that represents the area of a random shell of the solid (in terms of x).
Remember that each shell is a rectangle with two different sides: One side is the height of the function at x — that is, cos x. The other is the circumference of the solid at x — that is, 2πx. So to find the area of a shell, multiply these two numbers together:
A = 2πx cos x
Use this expression to build a definite integral (in terms of dx) that represents the volume of the solid.
In this case, remember that you’re adding up all the shells from the center (at x = 0) to the outer edge
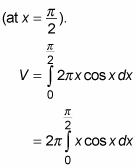
Evaluate the integral.
This integral is pretty easy to solve using integration by parts:
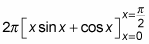
Now evaluate this expression:
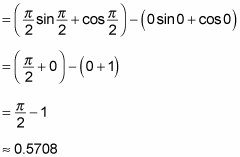
So the volume of the solid is approximately 0.5708 cubic units.

