The Mean Value Theorem for Integrals guarantees that for every definite integral, a rectangle with the same area and width exists. Moreover, if you superimpose this rectangle on the definite integral, the top of the rectangle intersects the function. This rectangle, by the way, is called the mean-value rectangle for that definite integral. Its existence allows you to calculate the average value of the definite integral.
Calculus boasts two Mean Value Theorems — one for derivatives and one for integrals. Here, you will look at the Mean Value Theorem for Integrals. You can find out about the Mean Value Theorem for Derivatives in Calculus For Dummies by Mark Ryan (Wiley).
The best way to see how this theorem works is with a visual example:
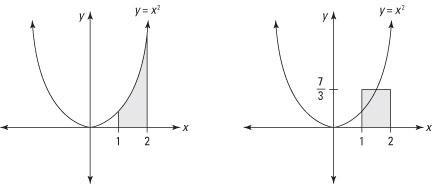
The first graph in the figure shows the region described by the definite integral
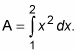
This region obviously has a width of 1, and you can evaluate it easily to show that its area is
The second graph in the figure shows a rectangle with a width of 1 and an area of
It should come as no surprise that this rectangle’s height is also
so the top of this rectangle intersects the original function.
The fact that the top of the mean-value rectangle intersects the function is mostly a matter of common sense. After all, the height of this rectangle represents the average value that the function attains over a given interval. This value must fall someplace between the function’s maximum and minimum values on that interval.
Here’s the formal statement of the Mean Value Theorem for Integrals: If f(x) is a continuous function on the closed interval [a, b], then there exists a number c in that interval such that:
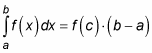
This equation may look complicated, but it’s basically a restatement of this familiar equation for the area of a rectangle:
Area = Height · Width
In other words, start with a definite integral that expresses an area, and then draw a rectangle of equal area with the same width (b – a). The height of that rectangle — f(c) — is such that its top edge intersects the function where x = c.
The value f(c) is the average value of f(x) over the interval [a, b]. You can calculate it by rearranging the equation stated in the theorem:
![The value f(c) is the average value of f(x) over the interval [a, b]](https://www.dummies.com/wp-content/uploads/312090.image6.png)
For example, here’s a figure that illustrates the definite integral
and its mean-value rectangle.
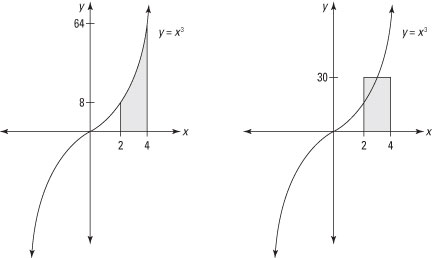
Now, here’s how you calculate the average value of the shaded area:
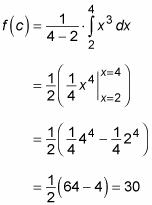
Not surprisingly, the average value of this integral is 30, a value between the function’s minimum of 8 and its maximum of 64.

