The direct comparison test is a simple, common-sense rule: If you’ve got a series that’s smaller than a convergent benchmark series, then your series must also converge. And if your series is larger than a divergent benchmark series, then your series must also diverge. Here's the mumbo jumbo.
Direct Comparison Test:
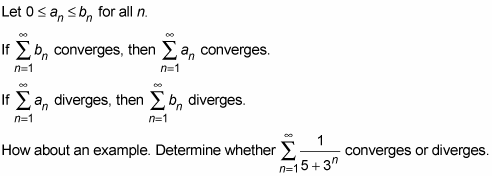
Piece o’ cake. This series resembles

(Note that you can rewrite this in the standard geometric series form as
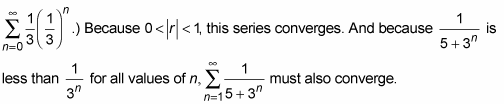
Here’s another one: Does

For any of the convergence/divergence tests, you can disregard any number of terms at the beginning of a series. And if you’re comparing two series, you can ignore any number of terms from the beginning of either or both of the series — and you can ignore a different number of terms in each of the two series.
This utter disregard of innocent beginning terms is allowed because the first, say, 10 or 1000 or 1,000,000 terms of a series always sum to a finite number and thus never have any effect on whether the series converges or diverges. Note, however, that disregarding a number of terms would affect the total that a convergent series converges to.
The direct comparison test tells you nothing if the series you’re investigating is bigger than a known convergent series or smaller than a known divergent series.
For example, say you want to determine whether

The p-series test says that this series diverges, but that doesn’t help you because your series is smaller than this known divergent benchmark.
Instead, you should compare your series to the divergent harmonic series,
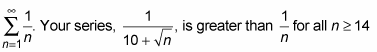
(it takes a little work to show this; give it a try). Because your series is greater than the divergent harmonic series, your series must also diverge.

