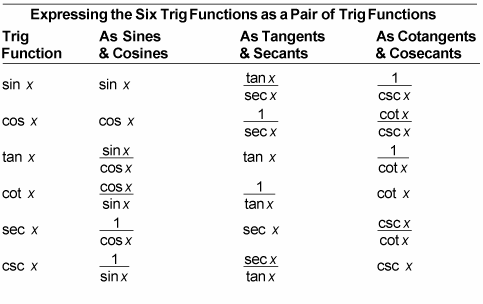
You can express every product of powers of trig functions, no matter how weird, as the product of any pair of trig functions. The three most useful pairings are sine and cosine, tangent and secant, and cotangent and cosecant. The table shows you how to express all six trig functions as each of these pairings.
For example, look at the following function:
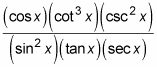
As it stands, you can’t do much to integrate this monster. But try expressing it in terms of each possible pairing of trig functions:
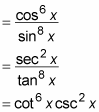
As it turns out, the most useful pairing for integration in this case is cot6 x csc2 x. No fraction is present — that is, both terms are raised to positive powers — and the cosecant term is raised to an even power.

