You can use a shortcut to integrate compositions of functions — that is, nested functions of the form f(g(x)). Technically, you’re using the variable substitution u = g(x), but you can bypass this step and still get the right answer.
This shortcut works for compositions of functions f(g(x)) for which
You know how to integrate the outer function f.
The inner function g(x) is of the form ax or ax + b — that is, it differentiates to a constant.
When these two conditions hold, you can integrate f(g(x)) by using the following three steps:
Write down the reciprocal of the coefficient of x.
Multiply by the integral of the outer function, copying the inner function as you would when using the Chain Rule in differentiation.
Add C.
Here’s an example:
Notice that this is a function nested within a function, where the following are true:
The outer function f is the cosine function.
The inner function is g(x) = 4x, which is of the form ax.
So you can integrate this function quickly as follows:
Write down the reciprocal of 4:
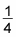
Multiply this reciprocal by the integral of the outer function, copying the inner function:
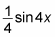
Add C:
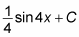
That’s it! You can check this easily by differentiating, using the Chain Rule:
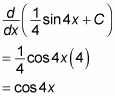
Here’s another example:
Remember as you begin that sec2 10x dx is a notational shorthand for [sec (10x)]2. So the outer function f is the sec2 function and the inner function is g(x) = 10x. The criteria for variable substitution are met, so make your way through the steps:
Write down the reciprocal of 10:
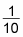
Multiply this reciprocal by the integral of the outer function, copying the inner function:
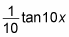
Add C:
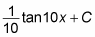
Here’s the check:
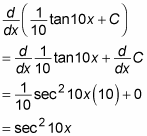
Take a look at another example:
In this case, the outer function is division, which counts as a function (technically speaking f(x) = x–1). The inner function is 7x + 2. Both of these functions meet the criteria, so here’s how to perform this integration:
Write down the reciprocal of the coefficient 7:
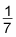
Multiply this reciprocal by the integral of the outer function, copying the inner function:
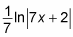
Add C:
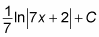
You’re done! You can check your result by differentiating, using the Chain Rule:
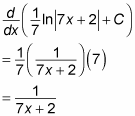
Consider one more example:
This time, the outer function f is a square root — that is, an exponent of 1/2 — and g(x) = 12x – 5, so you can use a quick substitution:
Write down the reciprocal of 12:
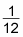
Multiply the integral of the outer function, copying down the inner function:
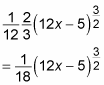
Add C:
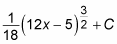
The table gives you a variety of integrals of the form f(g(x)). As you look over this chart, get a sense of the pattern so that you can spot it when you have an opportunity to integrate quickly.


