Variable substitution helps to fill the gaps left by the absence of a Product Rule and a Chain Rule for integration.
Here’s a hairy-looking integral that actually responds well to substitution:
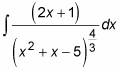
The key insight here is that the numerator of this fraction is the derivative of the inner function in the denominator. Watch how this plays out in this substitution:
-
Declare u equal to the inner function in the denominator and make the substitution:
Here’s the substitution:
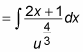
-
Differential du = (2x + 1) dx:
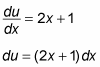
-
The second part of the substitution now becomes clear:
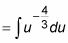
Notice how this substitution hinges on the fact that the numerator is the derivative of the inner function in the denominator. (You may think that this is quite a coincidence, but coincidences like these happen all the time on exams!)
-
Integration is now quite straightforward:
You take an extra step to remove the fraction before you integrate:
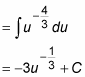
-
Substitute back x2 + x – 5 for u:
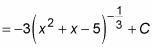
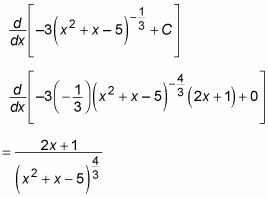
Here’s another example where you make a variable substitution:
Notice that the derivative of x4 – 1 is x3, off by a constant factor. So here’s the declaration, followed by the differentiation:
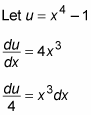
Now you can just do both substitutions at once:
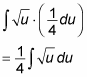
At this point, you can solve the integral simply.
Similarly, here’s another example:
At first glance, this integral looks just plain horrible. But on further inspection, notice that the derivative of cot x is –csc2 x, so this looks like another good candidate:
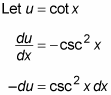
This results in the following substitution:
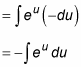
Again, this is another integral that you can solve.

