A clever method for solving differential equations (DEs) is in the form of a linear first-order equation. This method involves multiplying the entire equation by an integrating factor. A linear first-order equation takes the following form:
To use this method, follow these steps:
Calculate the integrating factor.
Multiply the DE by this integrating factor.
Restate the left side of the equation as a single derivative.
Integrate both sides of the equation and solve for y.
To help you understand how multiplying by an integrating factor works, the following equation is set up to practically solve itself — that is, if you know what to do:
Notice that this is a linear first-degree DE, with
and b(x) = 0. You now tweak this equation by multiplying every term by x2 (you see why shortly):
Next, you use algebra to do a little simplifying and rearranging:
Here’s where you appear to get extremely lucky: The two terms on the left side of the equation just happen to be the result of the application of the Product Rule to the expression y · x2:
Notice that the right side of this equation is exactly the same as the left side of the previous equation. So you can make the following substitution:
Now, to undo the derivative on the left side, you integrate both sides, and then you solve for y:
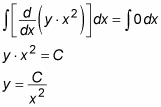
To check this solution, you plug this value of y back into the original equation:
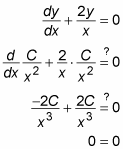
The previous example works because you found a way to multiply the entire equation by a factor that made the left side of the equation look like a derivative resulting from the Product Rule. Although this looked lucky, if you know what to multiply by, every linear first-order DE can be transformed in this way. Recall that the form of a linear first-order DE is as follows:
The trick is to multiply the DE by an integrating factor based on a(x). Here’s the integrating factor:
For example, in the previous problem, you know that
So here’s how to find the integrating factor:
Remember that 2 ln x = ln x2, so:
As you can see, the integrating factor x2 is the exact value that you multiplied by to solve the problem. To see how this process works now that you know the trick, here’s another DE to solve:
In this case, a(x) = 3, so compute the integrating factor as follows:
Now multiply every term in the equation by this factor:
If you like, use algebra to simplify the right side and rearrange the left side:
Now you can see how the left side of this equation looks like the result of the Product Rule applied to evaluate the following derivative:
Because the right side of this equation is the same as the left side of the previous equation, you can make the following substitution:
Notice that you change the left side of the equation using the Product Rule in reverse. That is, you’re expressing the whole left side as a single derivative. Now you can integrate both sides to undo this derivative:
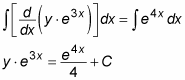
Now solve for y and simplify:
To check this answer, substitute this value of y back into the original DE:
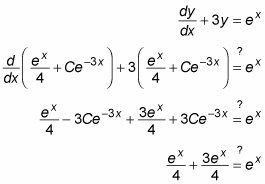
As if by magic, this answer checks out, so the solution is valid.

