The hypotenuse is the longest side in a right triangle, which is different from the long leg. The long leg is the leg opposite the 60-degree angle.
Two of the most common right triangles are 30-60-90 and the 45-45-90-degree triangles. All 30-60-90 triangles have sides with the same basic ratio. If you look at the 30–60–90-degree triangle in radians, it translates to the following:The figure illustrates the ratio of the sides for the 30-60-90-degree triangle.
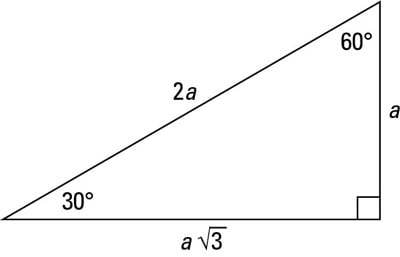 A 30-60-90-degree right triangle
A 30-60-90-degree right triangle-
Type 1: You know the short leg (the side across from the 30-degree angle). Double its length to find the hypotenuse. You can multiply the short side by the square root of 3 to find the long leg.
-
Type 2: You know the hypotenuse. Divide the hypotenuse by 2 to find the short side. Multiply this answer by the square root of 3 to find the long leg.
-
Type 3: You know the long leg (the side across from the 60-degree angle). Divide this side by the square root of 3 to find the short side. Double that figure to find the hypotenuse.
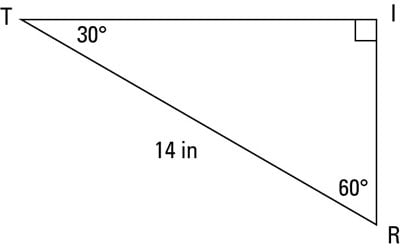 Finding the other sides of a 30-60-90 triangle when you know the hypotenuse
Finding the other sides of a 30-60-90 triangle when you know the hypotenuse
Because you have the hypotenuse TR = 14, you can divide by 2 to get the short side: RI = 7. Now you multiply this length by the square root of 3 to get the long side:

