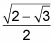You can use half-angle identities to evaluate a trig function of an angle that isn't on the unit circle by using one that is. For example, 15 degrees, which isn't on the unit circle, is half of 30 degrees, which is on the unit circle.
Cutting special angles on the unit circle in half gives you a variety of new angles that can't be achieved by using the sum and difference formulas or the double-angle formulas. Although the half-angle formulas won't give you all the angles of the unit circle, they certainly get you closer than you were before.
The trick is knowing which type of identity serves your purpose best. Half-angle formulas are the better option when you need to find the trig values for any angle that can be expressed as half of another angle on the unit circle. For example, to evaluate a trig function of pi/8, you can apply the half-angle formula to pi/4. Because no combination of sums or differences of special angles gets you pi/8, you know to use a half-angle formula.
You also can find the values of trig functions for angles like pi/12, each of which are exactly half of angles on the unit circle. Of course, these angles aren't the only types that the identities work for. You can continue to halve any angle on the unit circle for the rest of your life (if you have nothing better to do) and take the trig functions of those angles. For example, 15 degrees is half of 30 degrees, and 7.5 degrees is half of 15 degrees.
The half-angle formulas for sine, cosine, and tangent are as follows:
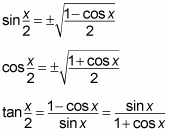
In the half-angle formula for sine and cosine, notice that a plus/minus sign appears in front of each radical (square root). Whether your answer is positive or negative depends on which quadrant the new angle (the half angle) is in. The half-angle formula for tangent doesn't have a plus/minus sign in front, so the above doesn't apply to tangent.
For example, to find sin 165º, follow these steps:
Rewrite the trig function and the angle as half of a unit circle value.
First realize that 165 degrees is half of 330 degrees, so you can rewrite the sine function as sin(330/2).
Determine the sign of the trig function.
Because 165 degrees is in quadrant II of the coordinate plane, its sine value should be positive.
Substitute the angle value into the right identity.
The angle value 330 degrees plugs in for x in the positive half-angle formula for sine. This gives you
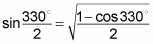
Replace cos x with its actual value.
Use the unit circle to find cos 330 degrees. Substituting that value into the equation gives you
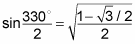
Simplify the half-angle formula to solve.
This approach has three steps:
Find the common denominator for the two fractions on top (including 1/1) to get
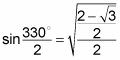
Use the rules for dividing fractions to get
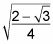
Finally, the square of the bottom simplifies to 2, and you end up with