Finding the maximum or minimum value of a real-world function is one of the most practical uses of differentiation. For example, you might need to find the maximum area of a corral, given a certain length of fencing.
Say that a rancher can afford 300 feet of fencing to build a corral that’s divided into two equal rectangles. What dimensions will maximize the corral’s area? The rancher wants to give his animals as much room as possible by using the length of fencing that he can afford. Like all businesspeople, he wants the most bang for his buck:
Express the thing you want maximized, the area, as a function of the two unknowns, x and y.
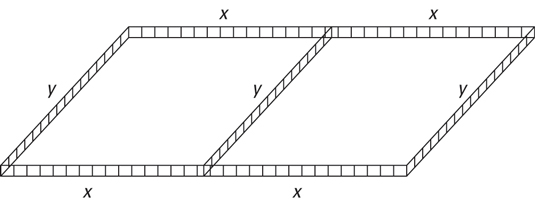
A = l · w
= (2x)(y)
Because the area is a function of two variables, Step 1 has two additional sub-steps.
Use the given information to relate the two unknowns to each other.
The fencing is used for seven sections, thus
300 = x + x + x + x + y + y + y
300 = 4x + 3y
Solve this equation for y, and plug the result into the y in the equation from Step 1. This gives you what you need — a function of one variable.
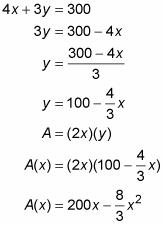
Determine the domain of the function.
You can’t have a negative length of fence, so x can’t be negative, and the most x can be is 300 divided by 4, or 75. Thus, the domain is 0 ≤ x ≤ 75.
Find the critical numbers of A(x) in the open interval (0, 75) by setting its derivative equal to zero and solving.
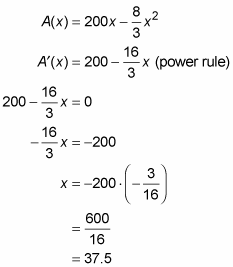
Because A′ is defined for all x-values, 37.5 is the only critical number.
Evaluate the function at the critical number, 37.5, and at the endpoints of the interval, 0 and 75.
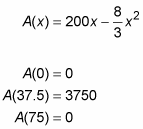
Keep in mind that evaluating a function at the endpoints of an interval is a standard step in finding an absolute extremum on the interval. However, you could have skipped this step here had you noticed that A(x) is an upside-down parabola and that, therefore, its peak must be higher than either endpoint.
The maximum value in the interval is 3750, and thus, an x-value of 37.5 feet maximizes the corral’s area. The length is 2x, or 75 feet. The width is y, which equals
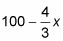
Plugging in 37.5 gives you
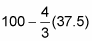
or 50 feet. So the rancher will build a 75-foot by 50-foot corral with an area of 3750 square feet.
This is a real-world situation where it pays to do the math. Had the rancher not solved this problem, he would likely have built an inferior, smaller corral. Many people know that a square often maximizes area (this would be the case, for example, in a similar corral problem where there is no dividing fence in the middle of the corral). So, the rancher might have thought that he should build a square corral or, perhaps a rectangular corral made up of two squares. These two corrals would have total areas of, respectively, 3600 square feet and 3673 square feet. Granted, the lost area is not substantial in either case, but why cramp his animals even a little for no reason? And, in other problems, failing to find an exact maximum or minimum can have much more significant consequences.

