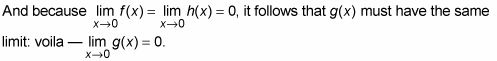When you can't solve a limit by using algebra, try making a limit sandwich. The best way to understand the sandwich, or squeeze, method is by looking at a graph.
Look at functions f, g, and h in the figure: g is sandwiched between f and h. If near the x-number — 2 in this example — f is always higher than or the same height as g, and g is always higher than or the same height as h, and so you can use the sandwich theorem:

The limit of both f and h as x approaches 2 is 3. So, 3 has to be the limit of g as well. It’s got nowhere else to go. Here’s another example:
Try substitution (always try substitution first).

No good, can’t divide by zero. On to plan B.
Try algebraic methods or any other tricks you have up your sleeve.
Knock yourself out. You can’t do it. Plan C.
Try your calculator.
(Note: the calculator instructions below are for a graphing calculator like the TI-84 or similar model. But if you use a different make of graphing calculator, you should be able to achieve the same results.)
It’s always a good idea to see what your calculator tells you even if this is a “show your work” problem. To graph this function, set your graphing calculator’s mode to radian and the window to
x min = –0.4
x max = 0.4
y min = –0.3
y max = 0.3
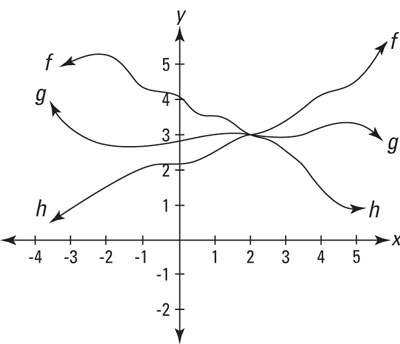
The next figure shows what the graph looks like.
It definitely looks like the limit of g is zero as x approaches zero from the left and the right. Now, check the table of values on your calculator (set TblStart to 0 and ∆Tbl to 0.001). The table below gives some of the values from the table that will appear on your calculator.

x g(x) 0 Error .001 .0008269 .002 –.000936 .003 .0009565 .004 –.003882 .005 –.004366 .006 –.000969 .007 –.006975 .008 –.004928 .009 –.008234 These function values sort of look like they’re getting closer and closer to zero as x gets close to zero, but they’re not convincing (note that when x gets closer to zero from 0.006 to 0.005, g gets further from zero). This type of table (using the automatic ∆Tbl) doesn’t work so great for oscillating functions like sine or cosine. So try the type of table described next.
Enter the function on your calculator's home screen and successively plug in the x-values listed in the table below to obtain the corresponding function values.

x g(x) .1 –.054 .01 –.0051 .001 .00083 .0001 –.000031 .00001 .00000036 Now you can definitely see that g is headed toward zero as x approaches zero.
Now you need to prove the limit mathematically, even though you’ve already solved it on your calculator. To do this, you need to make a limit sandwich.
The hard part about using the sandwich method is coming up with the “bread” functions (again, functions f and h are the bread and g is the salami). There’s no automatic way of doing this. You’ve got to think about the shape of the salami function, and then use your knowledge of functions and your imagination to come up with some good prospects for the bread functions.
Because the range of the sine function is from negative 1 to positive 1, whenever you multiply a number by the sine of anything, the result either stays the same distance from zero as that number or gets closer to zero.

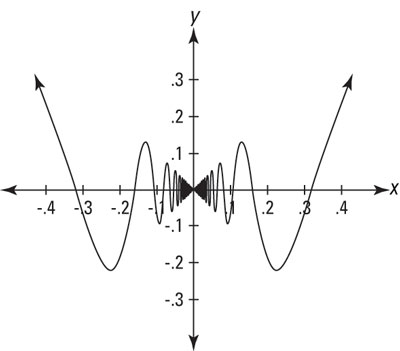
The next figure shows that they do.
You've shown — though perhaps not to a mathematician’s satisfaction, egad! — that
f (x) ≥ g (x) ≥ h (x).