In Calculus, you can use variable substitution to evaluate a complex integral. Variable substitution allows you to integrate when the Sum Rule, Constant Multiple Rule, and Power Rule don’t work.
Declare a variable u, set it equal to an algebraic expression that appears in the integral, and then substitute u for this expression in the integral.
Differentiate u to find
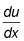
and then isolate all x variables on one side of the equal sign.
Make another substitution to change dx and all other occurrences of x in the integral to an expression that includes du.
Integrate by using u as your new variable of integration.
Express this answer in terms of x.

