The movement of a parent sine or cosine graph around the coordinate plane is a type of transformation known as a translation or a shift. For this type of transformation, every point on the parent graph is moved somewhere else on the coordinate plane. A translation doesn't affect the overall shape of the graph; it only changes its location on the plane. The following steps illustrate how to take the parent graphs of sine and cosine and shift them both horizontally and vertically.
Most math books write the horizontal and vertical shifts as y = sin(x – h) + v, or y = cos(x – h) + v. The variable h represents the horizontal shift of the graph, and v represents the vertical shift of the graph. The sign makes a difference in the direction of the movement. For example,
-
f(x) = sin(x – 3) moves the parent graph of y = sin x to the right by 3.
-
g(x) = cos(x + 2) moves the parent graph of y = cos x to the left by 2.
-
k(x) = sinx + 4 moves the parent graph of y = sin x up 4.
-
p(x) = cosx – 4 moves the parent graph of y = cos x down 4.
For example, if you need to graph
follow these steps:
-
Identify the parent graph.
You're looking at sine, so draw its parent graph. The starting value for the parent graph of

-
Shift the graph horizontally.
To find the new starting place, set what's inside the parentheses equal to the starting value of the parent graph:
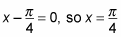
is where this graph starts its period. You move every point on the parent graph to the right by
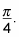
The figure shows what you have so far.
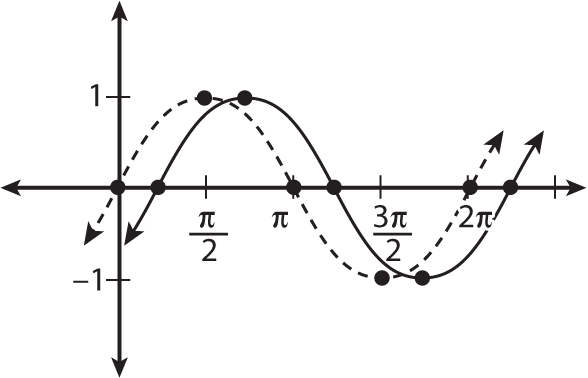 Shifting the parent graph of y = sin x to the right by pi/4.
Shifting the parent graph of y = sin x to the right by pi/4. -
Move the graph vertically.
The sinusoidal axis of the graph moves up three positions in this function, so shift all the points of the parent graph this direction now. You can see this shift in the next figure.
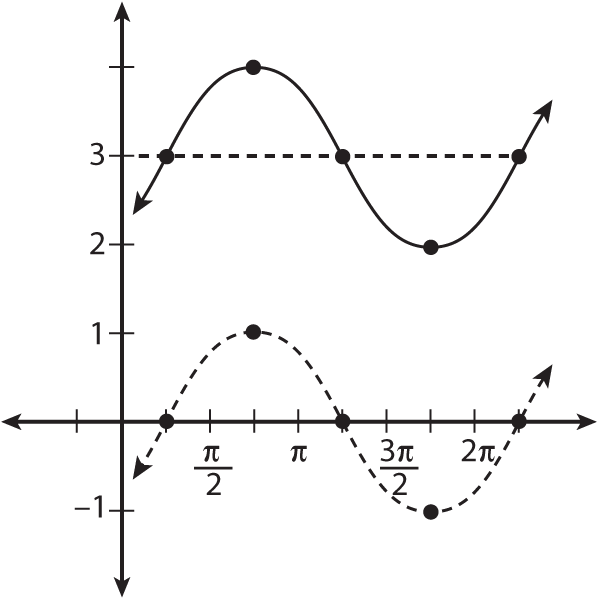 Moving the graph of y = sin(x – pi/4) up by three.
Moving the graph of y = sin(x – pi/4) up by three. -
State the domain and range of the transformed graph, if asked.
The domain and range of a function may be affected by a transformation. When this happens, you may be asked to state the new domain and range. Usually, you can visualize the range of the function easily by looking at the graph. Two factors that change the range are a vertical transformation (stretch or shrink) and a vertical translation.
Keep in mind that the range of the parent sine graph is [–1, 1]. Shifting the parent graph up three units makes the range of
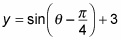
shift up three units also. Therefore, the new range is [2, 4]. The domain of this function isn't affected; it's still