You can take the unit-circle angles and the special right triangles and put them together to create a neat little package: the full unit circle. You create special triangles on the unit circle one at a time, because they're all points on the coordinate plane.
Regardless of how long the sides are that make up a particular angle in a triangle, the trigonometry function values for that specific angle are always the same. Therefore, mathematicians shrank all the sides of right triangles so that they'd all fit into the unit circle.
The hypotenuse of every triangle in a unit circle is always 1, making the calculations that involve the triangles much easier to compute. Because of the unit circle, you can draw any angle with any measurement, and all right triangles with the same reference angle are the same size.
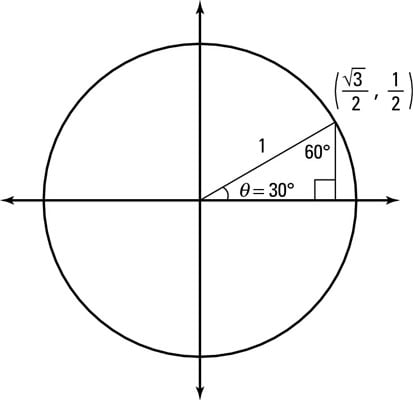
Starting in quadrant I, look at an angle marked 30 degrees in the unit circle (shown in the previous figure):
Draw the angle and connect it to the origin, using a straight line.
The terminal side of a 30-degree angle should be in the first quadrant, and the size of the angle should be rather small. In fact, it should be one-third of the way between 0 degree and 90 degrees.
Draw a perpendicular line connecting the point where the ray stops to the x-axis, creating a right triangle.
The triangle's hypotenuse is the radius of the unit circle; one of its legs is on the x-axis; and the other leg is parallel to the y-axis. You can see what this 30-60-90-degree triangle looks like in the figure.
Find the length of the hypotenuse.
The radius of the unit circle is always 1, which means the hypotenuse of the triangle is also 1.
Find the lengths of the other sides.
To find the other two sides, you find the short leg first by dividing by 2, which gives you 1/2. To find the long leg, multiply 1/2 by

Identify the point on the unit circle.
The unit circle is on the coordinate plane, centered at the origin. So each of the points on the unit circle has unique coordinates. You can now name the point at 30 degrees on the circle:
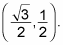
After going through these steps, you can easily find the points of other angles on the unit circle as well. For instance:
Look at the point on the circle marked 45 degrees. You can draw a triangle from it, using Steps 1 and 2. Its hypotenuse is still 1, the radius of the unit circle. To find the length of the legs of a 45-45-90-degree triangle, you divide the hypotenuse by
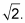
You then rationalize the denominator to get
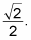
You can now name this point on the circle
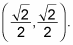
Moving counterclockwise to the 60-degree angle, you can create a triangle with Steps 1 and 2. If you look closely, you'll realize that this is a 30-60-90 triangle with the 30-degree angle at the top, so the short side is the side on the x-axis. That makes the point at 60-degrees
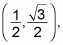
and because the radius is 1, (divide 1 by 2 to get the length of the short side as 1/2). Then multiply 1/2 by
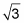
to get the length of the long side as
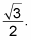
Quadrants II to IV in the coordinate plane are just mirror images of the first quadrant. However, the signs are different because the points on the unit circle are on different locations of the plane:
In quadrant I, both x and y values are positive.
In quadrant II, x is negative and y is positive.
In quadrant III, both x and y are negative.
In quadrant IV, x is positive and y is negative.
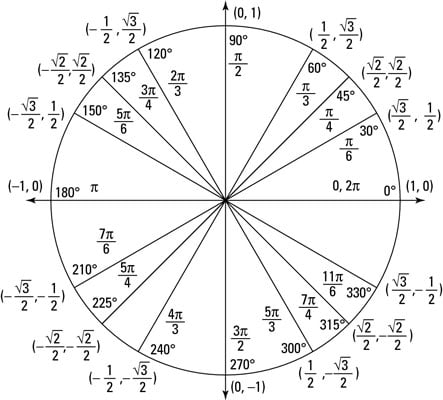 The whole unit circle.
The whole unit circle.
The good news is that you never have to memorize the whole unit circle. You can simply apply the basics of what you know about right triangles and the unit circle! The preceding figure shows the whole pizza pie of the unit circle.

