You’re going to see dozens and dozens of functions in your study of calculus, and the graphs of those functions can visually express such things as inflation, population growth, and radioactive decay. Below are some of the most common types of functions:
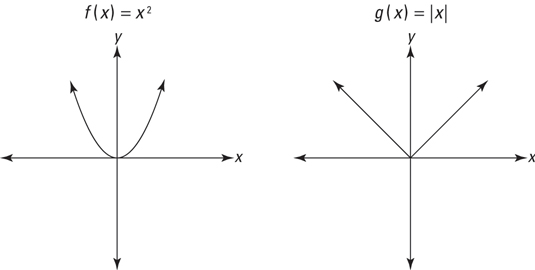
Parabolic and absolute value functions: In this figure, both functions are symmetric with respect to the y-axis. In other words, the left and right sides of each graph are mirror images of each other, which makes them even functions.
A couple oddball functions: Graph these two equations on your graphing calculator:
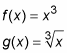
These two functions illustrate odd symmetry. Odd functions are symmetric with respect to the origin, which means that if you rotate them 180 degrees around the origin, they will land on themselves. A polynomial function like
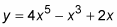
where all powers of x are odd, is one type of odd function.
Many functions are neither even nor odd — for example:
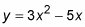
Note that a function like
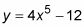
is also neither even nor odd because the first term has an odd degree, but the second term, the 12, has an even degree of zero (you can think of it as 12 times x raised to the zero power).
Also note that the even and odd degree rule works only for polynomial functions. For example, y = cos(x) is an even function despite the fact that the power on x is one. (y = sin(x) happens to be an odd function).
Exponential functions: An exponential function is one with a power that contains a variable, such as:
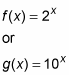
Take a look at the following figure.
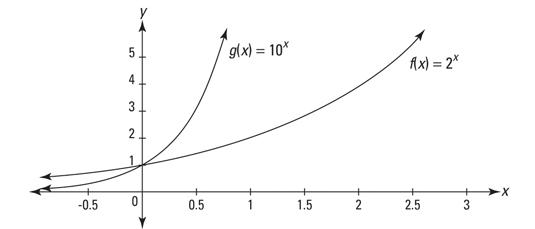
Both functions go through the point (0, 1), as do all exponential functions of the form
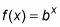
When b is greater than 1, you have exponential growth. All such functions go up to the right forever, and as they go left toward negative infinity, they crawl along the x-axis, always getting closer, but never touching the axis. You use these and related functions for analyzing things such as investments, inflation, and growing population.
When b is less than 1, you have an exponential decay function. The graphs of such functions are like exponential growth functions in reverse. Exponential decay functions also cross the y-axis at (0, 1), but they go up to the left forever, and crawl along the x-axis to the right. These functions model things that shrink over time, such as the radioactive decay of uranium.
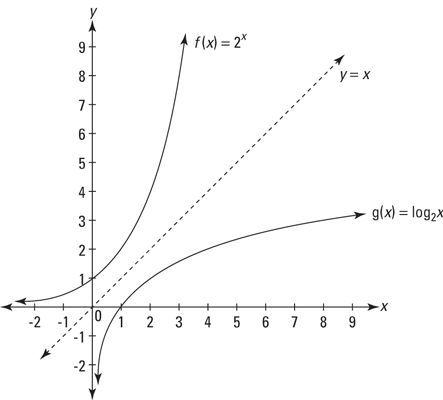
Logarithmic functions: A logarithmic function is simply an exponential function with the x and y axes switched. In other words, the up-and-down direction on an exponential graph corresponds to the right-and-left direction on a logarithmic graph, and the right-and-left direction on an exponential graph corresponds to the up-and-down direction on a logarithmic graph. You can see this relationship in the figure above, which shows, graphed on the same set of axes,
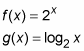
The two functions are mirror images of each other with respect to the line y = x. This makes them inverses of each other.

