-
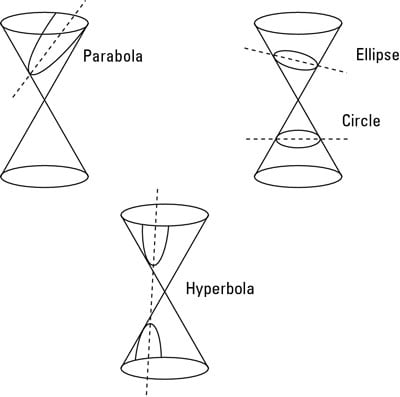
Circle: A circle is the set of all points that are a given distance (the radius, r) from a given point (the center). To get a circle from the right cone, the plane slices occurs horizontally through either the top or bottom half of the cone.
-
Parabola: A parabola is a curve in which every point is equidistant from one point (the focus) and a line (the directrix). It looks a lot like the letter U, although it may be upside down or sideways. To form a parabola, the plane slices through parallel to the side of the right cone).
-
Ellipse: An ellipse is the set of all points where the sum of the distances from two points (the foci) is constant. You may be more familiar with another term for ellipse, oval. In order to get an ellipse from the right cone, the plane must slice through the cone at a shallow enough angle where it is slicing through only one-half of the cone. (Note: if the plane slices horizontally through the cone, a circle is created. A circle is considered a special type of ellipse.)
-
Hyperbola: A hyperbola is the set of points where the difference of the distances between two points is constant. The shape of the hyperbola is difficult to describe without a picture, but it looks visually like two parabolas (although they're very different mathematically) mirroring one another with some space between them. To get a hyperbola, the plane must slice through the right cone and a steep enough angle where it is slicing through both halves of the cone.
Most of the time, sketching a conic is not enough. Each conic section has its own set of information that you usually have to give to supplement the graph. You have to indicate where the center, vertices, major and minor axes, and foci are located. Often, this information is more important than the graph itself. Besides, knowing all this valuable info helps you sketch the graph more accurately than you could without it.

