Sometimes your pre-calculus teacher may ask you to graph conics in parametric form. Parametric form is a fancy way of saying a form in which you can deal with conics that aren't easily expressed as the graph of a function y = f(x). Parametric equations are usually used to describe the motion or velocity of an object with respect to time. Using parametric equations allows you to evaluate both x and y as dependent variables, as opposed to x being independent and y dependent on x.
Parametric form defines both the x- and the y-variables of conic sections in terms of a third, arbitrary variable, called the parameter, which is usually represented by t. You can find values for both x and y by plugging values for t into the parametric equations. As the values for t change, so do the values for x and y, which means that y is no longer dependent on x but is dependent on t.
Why switch to this form? Consider, for example, an object moving in a plane during a specific time interval. If a problem asks you to describe the path of the object and its location at any certain time, you need three variables:
Time t, which usually is the parameter
The coordinates (x, y) of the object at time t
The xt equation gives the horizontal movement of an object as t changes; the yt equation gives the vertical movement of an object over time.
For example, one set of equations defines both x and y for the same parameter — t — and defines the parameter in a set interval:
Time t exists only between 1 and 5 seconds for this problem.
If you're asked to graph this equation, you can do it in one of two ways. The first method is the plug and chug: Set up a chart and pick t values from the given interval in order to figure out what x and y should be, and then graph these points like normal. The following table shows the results of this process. Note: t = 1 is included in the chart, even though the parameter isn't defined there. You need to see what it would've been, because you graph the point where t = 1 with an open circle to show what happens to the function arbitrarily close to 1. Be sure to make that point an open circle on your graph.
The other way to graph a parametric curve is to solve one equation for the parameter and then substitute that equation into the other equation. You should pick the simplest equation to solve and start there.
Sticking with the same example, solve the linear equation x = 2t – 1 for t:
Substitute the endpoints of the t interval into the x function to know where the graph starts and stops.
This is done in the table. When t = 1, x = 1, and when t = 5, x = 9.
Solve the simplest equation.
For the chosen equation, you get
Plug the solved equation into the other equation.
For this step, you get
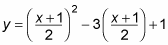
Simplify this equation if necessary.
You now have
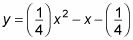
Because this step gives you an equation in terms of x and y, you can graph the points on the coordinate plane. The only problem is that you don't draw the entire graph, because you have to look at a specific interval of t.
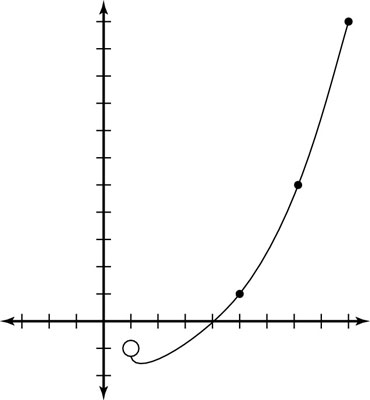 Graphing a parametric curve.
Graphing a parametric curve.
This figure shows the parametric curve from this example (for both methods). You end up with a parabola, but you can also write parametric equations for ellipses, circles, and hyperbolas.

