To graph complex numbers, you simply combine the ideas of the real-number coordinate plane and the Gauss or Argand coordinate plane to create the complex coordinate plane. In other words, given a complex number A+Bi, you take the real portion of the complex number (A) to represent the x-coordinate, and you take the imaginary portion (B) to represent the y-coordinate.
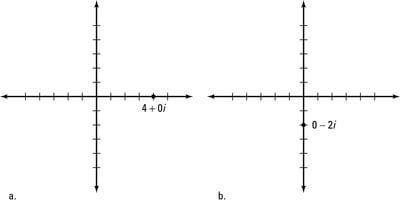
In the Gauss or Argand coordinate plane, pure real numbers in the form a + 0i exist completely on the real axis (the horizontal axis), and pure imaginary numbers in the form 0 + Bi exist completely on the imaginary axis (the vertical axis). Figure a shows the graph of a real number, and Figure b shows that of an imaginary number.
Although you graph complex numbers much like any point in the real-number coordinate plane, complex numbers aren't real! The x-coordinate is the only real part of a complex number, so you call the x-axis the real axis and the y-axis the imaginary axis when graphing in the complex coordinate plane.
Graphing complex numbers gives you a way to visualize them, but a graphed complex number doesn't have the same physical significance as a real-number coordinate pair. For an (x, y) coordinate, the position of the point on the plane is represented by two numbers. In the complex plane, the value of a single complex number is represented by the position of the point, so each complex number A + Bi can be expressed as the ordered pair (A, B).
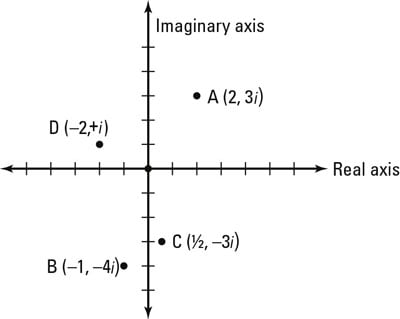
You can see several examples of graphed complex numbers in this figure:
Point A. The real part is 2 and the imaginary part is 3, so the complex coordinate is (2, 3) where 2 is on the real (or horizontal) axis and 3 is on the imaginary (or vertical) axis. This point is 2 + 3i.
Point B. The real part is –1 and the imaginary part is –4; you can draw the point on the complex plane as (–1, –4). This point is –1 – 4i.
Point C. The real part is 1/2 and the imaginary part is –3, so the complex coordinate is (1/2, –3). This point is 1/2 – 3i.
Point D. The real part is –2 and the imaginary part is 1, which means that on the complex plane, the point is (–2, 1). This coordinate is –2 + i.

