In order to graph a parabola correctly, it is important to note whether it is a horizontal or a vertical parabola. This is because while the variables and constants in the equations for both curves serve the same purpose, their effect on the graphs in the end is slightly different.
A vertical parabola has its axis of symmetry at x = h, and the vertex is (h, v). With this information, you can find the focus and directrix.
The focus is the distance from the vertex to the focus is 1/(4a), where a can be found in the equation of the parabola (it is the scalar in front of the parentheses). The focus, as a point, is (h, v + 1/(4a)); it should be directly above or directly below the vertex. It always appears inside the parabola.
The equation of the directrix is y = v – 1/(4a). It should be the same distance from the vertex along the axis of symmetry as the focus, in the opposite direction. The directrix appears outside the parabola and is perpendicular to the axis of symmetry. Because the axis of symmetry is vertical, the directrix is a horizontal line; thus, it has an equation of the form y = a constant, which is v – 1/(4a).
Square the variables in the equation of the parabola.
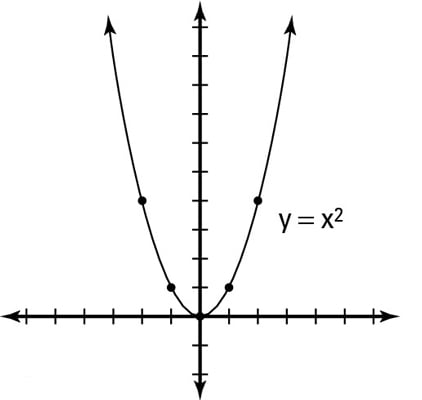
The squaring of the variables in the equation of the parabola determines where it opens: When the x is squared and y is not, the axis of symmetry is vertical and the parabola opens up or down. For instance, y = x2 is a vertical parabola; its graph is shown.
Deal with negative coefficients in parabolas.
Be aware of negative coefficients in parabolas. If the parabola is vertical, a negative coefficient will make the parabola open downward.
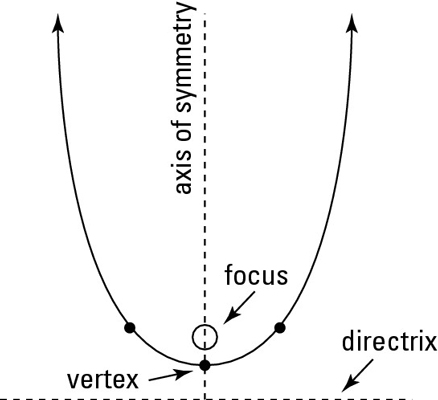
The figure can be referred to as the “martini” of parabolas. The graph looks like a martini glass: The axis of symmetry is the glass stem, the directrix is the base of the glass, and the focus is the olive. You need all those parts to make a good martini and a parabola.
Find the parabola's parts and create vertical parabola.
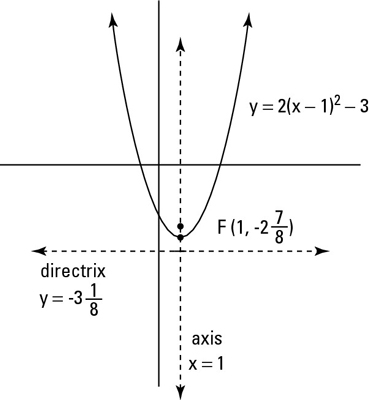
For example, the equation y = 2(x – 1)2 – 3, has its vertex at (1, –3). This means that a = 2, h = 1, and v = –3. With this information, you can identify all the parts of a parabola (axis of symmetry, focus, and directrix) as points or equations:
First, find the axis of symmetry. The axis of symmetry is at x = h, which means that x = 1.
Second, determine the focal distance and write the focus as a point. You can find the focal distance by using the formula 1/(4a). Because a = 2, the focal distance for this parabola is 1/8. With this distance, you can write the focus as the point (h,v + 1/4a), or (1,–2-7/8)
Third, find the directrix. You can use the equation of the directrix: y = v – 1/4a, or y = –3-1/8.
Last, graph the parabola and label all its parts as shown.
It is always a good idea to plot at least two other points besides the vertex so that you can show that your vertical transformation is correct. Because the vertical transformation in this equation is a factor of 2, the two points on both sides of the vertex will be stretched by a factor of two.
So, from the vertex, you plot a point that is to the right one, and up two (instead of up one). Then you can draw the same point on the other side of the axis of symmetry; the two other points on the graph are at (2, –1) and (0, –1).

