Knowing how to graph trig functions allows you to measure the movement of objects that move back and forth or up and down in a regular interval, such as pendulums. Sine functions are perfect ways of expressing this type of movement, because their graphs are repetitive and they oscillate (like a wave).
The waves crest and fall over and over again forever, because you can keep plugging in values for
for the rest of your life. The following steps show you how to construct the parent graph for the sine function,
Keep in mind that because all the values of the sine function come from the unit circle, you should be pretty comfy and cozy with the unit circle before proceeding. You can graph any trig function in four or five steps. Here are the steps to construct the graph of the parent function
Because the graph of the sine function is being graphed on the x-y plane, you rewrite this as f(x) = sin x where x is the measure of the angle in radians.
Find the values for domain and range.
No matter what you put into the sine function, you get an answer as output, because
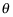
can rotate around the unit circle in either direction an infinite number of times. Therefore, the domain of sine is all real numbers, or
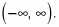
On the unit circle, the y values are your sine values — what you get after plugging the value of
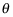
into the sine function. Because the radius of the unit circle is 1, the y values can't be more than 1 or less than negative 1 — your range for the sine function. So in the x-direction, the wave (or sinusoid, in math language) goes on forever, and in the y-direction, the sinusoid oscillates only between –1 and 1, including these values. In interval notation, you write this as [–1, 1].
Calculate the graph's x-intercepts.
When you graph lines in algebra, the x-intercepts occur when y = 0. Find out where the graph of f(x) = sin x crosses the x-axis by finding unit circle angles where sine is 0. We see that the graph of f(x) = sin x crosses the x-axis three times:
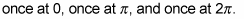
You now know that three of the coordinate points are
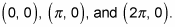
Calculate the graph's maximum and minimum points.
To complete this step, use your knowledge of the range from Step 1. You know that the highest value that sin x can be is 1. At what angles(s) does this happen?
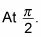
You now have another coordinate point at
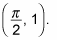
You also can see that the lowest value of sin x can be is –1, when the angle x is
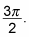
Hence, you have another coordinate point:
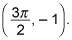
Sketch the graph of the function.
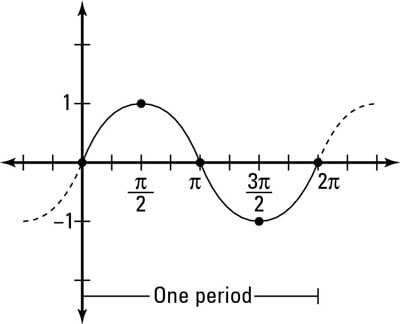
Using the five key points as a guide, connect the points with a smooth, round curve. The figure approximately shows the parent graph of sine,
Remember that the parent graph of the sine function has a couple of important characteristics worth noting:
It repeats itself every 2-pi radians. This repetition occurs because 2-pi radians is one trip around the unit circle — called the period of the sine graph — and after that, you start to go around again. Usually, you're asked to draw the graph to show one period of the function, because in this period you capture all possible values for sine before it starts repeating over and over again. The graph of sine is called periodic because of this repeating pattern.
It's symmetrical about the origin (thus, in math speak, it's an odd function). The sine function has 180-degree-point symmetry about the origin. If you look at it upside down, the graph looks exactly the same. The official math definition of an odd function, though, is f(–x) = –f(x) for every value of x in the domain. In other words, if you put in an opposite input, you'll get an opposite output. For example,


