Rational functions where the numerator has the greater degree don’t actually have horizontal asymptotes. Instead, they have oblique asymptotes which you find by using long division.
For example, graph h (x):
Sketch the vertical asymptote(s) of h (x).
Try to find the value for x in which the function is undefined. If you set the denominator equal to zero and solve for x, you get x = –2. You find only two intervals for this graph because there’s only one vertical asymptote — (–∞, –2) and (–2, ∞).
Sketch the oblique asymptote of h (x).
Because the numerator of this rational function has the greater degree, the function has an oblique asymptote. Use long division to find the oblique asymptote.
You take the denominator of the rational function and divide it into the numerator. The quotient (neglecting the remainder) gives you the equation of the line of your oblique asymptote.
You must understand long division of polynomials in order to complete the graph of a rational function with an oblique asymptote.
In this example, the oblique asymptote follows the equation y = x – 2.
Plot the x- and y-intercepts for h (x).
To find the y-intercept of an equation, set x = 0. (Plug in 0 wherever you see x.)
To find the x-intercept of an equation, set y = 0.
In this example, you find that the x-intercepts are ±3 and the y-intercept is –9/2.
Use test values of your choice to determine whether the graph is above or below the oblique asymptote.
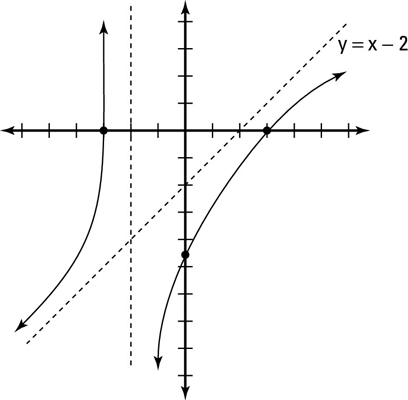
Notice that the intercepts conveniently give test points in each interval. In the first interval, the test point (–3, 0), hence the graph, is located above the oblique asymptote. In the second interval, the test points (0, –9/2) and (3, 0), as well as the graph, are located under the oblique asymptote. This figure shows the complete graph of h (x).

