When a function’s argument (that’s the function’s input) is more complicated than something like 3x + 2 (a linear function of x — that is, a function where x is raised to the first power), you can use the substitution method. This method works when the integrand contains a function and the derivative of the function’s argument — in other words, when it contains that extra thing produced by the chain rule — or something just like it except for a constant. And the integrand must not contain anything else. (If that sounds like gibberish, it’ll become clear when you read the following example).
Find the derivative of
with the substitution method.
Set u equal to the argument of the main function.
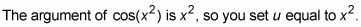
Take the derivative of u with respect to x.
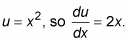
Solve for dx.

Make the substitutions.
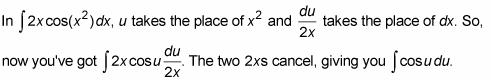
Antidifferentiate by using the simple reverse rule.
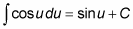
Substitute x-squared back in for u — coming full circle.
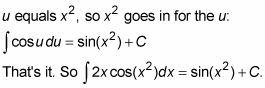
If the original problem had been

Now, you finish this problem just as you did in the preceding Steps 5 and 6, except for the extra 5/2.
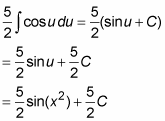
Because C is any old constant,

You should check this by differentiating it.

