The guess-and-check method works when the integrand — that’s the thing you want to antidifferentiate (the expression after the integral symbol, not counting the dx) — is close to a function that you know the reverse rule for. For example, say you want the antiderivative of cos(2x). Well, you know that the derivative of sine is cosine. Reversing that tells you that the antiderivative of cosine is sine. So you might think that the antiderivative of cos(2x) is sin(2x). That’s your guess. Now check it by differentiating it to see if you get the original function, cos(2x):

This result is very close to the original function, except for that extra coefficient of 2. In other words, the answer is 2 times as much as what you want. Because you want a result that’s half of this, just try an antiderivative that’s half of your first guess:
Check this second guess by differentiating it, and you get the desired result. Thus, the antiderivative of cos(2x) is

Guess the antiderivative.
This looks sort of like a power rule problem, so try the reverse power rule.

Check your guess by differentiating it.

Tweak your first guess.
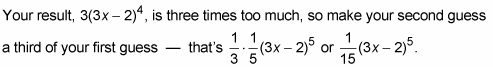
Check your second guess by differentiating it.
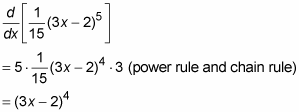
This answer checks — you’re done! The antiderivative of
The guess-and-check method works well when the function you want to antidifferentiate has an argument like 3x or 3x + 2 (where x is raised to the first power) instead of a plain old x.
You just have to tweak your guess by the reciprocal of the coefficient of x — the 3 in 3x + 2, for example (the 2 in 3x + 2 has no effect on your answer). In fact, for these easy problems, you don’t really have to do any guessing and checking. You can immediately see how to tweak your guess. It becomes sort of a one-step process.

