A line normal to a curve at a given point is the line perpendicular to the line that’s tangent at that same point. Find the points of perpendicularity for all normal lines to the parabola
that pass through the point (3, 15).
Graph the parabola and plot the point (3, 15). Now, before you do the math, try to approximate the locations of all normal lines. How many can you see? It’s pretty easy to see that, starting at (3, 15), one normal line goes down slightly to the right and another goes down a bit steeper toward the left. But did you find the third one that’s between these two? Don’t worry if you didn’t see this one because when you do the math, you get all three solutions.
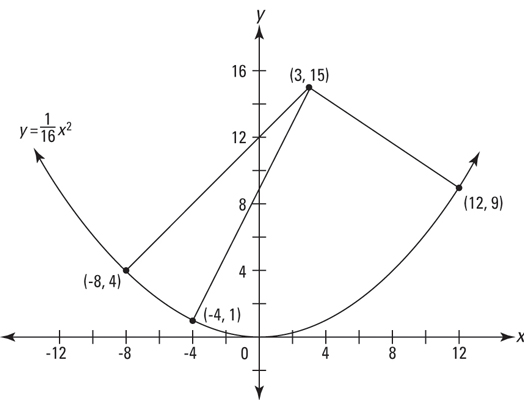
The figure shows the parabola and the three normal lines.
Looking at the figure, you can appreciate how practical this problem is. It’ll really come in handy if you happen to find yourself standing inside the curve of a parabolic wall, and you want to know the precise location of the three points on the wall where you could throw a ball and have it bounce straight back to you.
The solution is very similar to the solution of the tangent line problem, except that in this problem you use the rule for perpendicular lines:
The slopes of perpendicular lines are opposite reciprocals.
Each normal line in the figure is perpendicular to the tangent line drawn at the point where the normal meets the curve. So the slope of each normal line is the opposite reciprocal of the slope of the corresponding tangent — which, of course, is given by the derivative. So here goes.
Take a general point, (x, y), on the parabola
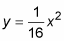
and substitute
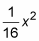
for y.

Take the derivative of the parabola.
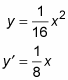
Using the slope formula, set the slope of each normal line from (3, 15) to
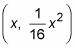
equal to the opposite reciprocal of the derivative at
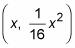
and solve for x.

Now, there’s no automatic way to get exact solutions to this cubic (3rd degree) equation like the way the quadratic formula gives you the solutions to a 2nd degree equation. Instead, you can graph
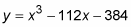
and the x-intercepts give you the solutions. (With this method, however, there’s no guarantee that you’ll get exact solutions; often, approximate solutions are the best you can do with cubic equations.) But in this problem you luck out and get the exact solutions of –8, –4, and 12.
Plug each of the x-coordinates (–8, –4, and 12) into
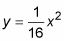
to obtain the y-coordinates.
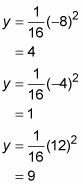
Thus, the three points of normalcy are (–8, 4), (–4, 1), and (12, 9).

