The chain rule is by far the trickiest derivative rule, but it’s not really that bad if you carefully focus on a few important points.

By the way, here’s one way to quickly recognize a composite function.
Whenever the argument of a function is anything other than a plain old x, you’ve got a composite function.

Here’s how to differentiate it with the chain rule:
You start with the outside function (the square root), and differentiate that, IGNORING what’s inside.
To make sure you ignore the inside, temporarily replace the inside function with the word stuff.

Multiply the result from Step 1 by the derivative of the inside function, stuff´.
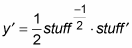
Take a good look at this. All basic chain rule problems follow this basic idea. You do the derivative rule for the outside function, ignoring the inside stuff, then multiply that by the derivative of the stuff.
Differentiate the inside stuff.
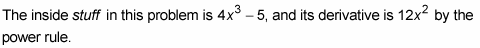
Put the real stuff and its derivative back where they belong.
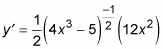
Simplify.


