The most complicated type of binomial expansion involves the complex number i, because you're not only dealing with the binomial theorem but dealing with imaginary numbers as well. When raising complex numbers to a power, note that i1 = i, i2 = –1, i3 = –i, and i4 = 1. If you run into higher powers, this pattern repeats: i5 = i, i6 = –1, i7 = –i, and so on. Because powers of the imaginary number i can be simplified, your final answer to the expansion should not include powers of i. Instead, use the information given here to simplify the powers of i and then combine your like terms.
For example, to expand (1 + 2i)8, follow these steps:
Write out the binomial expansion by using the binomial theorem, substituting in for the variables where necessary.
In case you forgot, here is the binomial theorem:
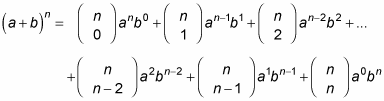
Using the theorem, (1 + 2i)8 expands to
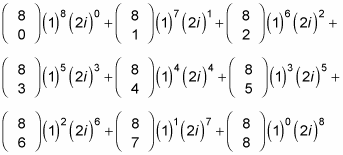
Find the binomial coefficients.
To do this, you use the formula for binomial expansion, which is written in the following form:
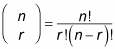
You may recall the term factorial from your earlier math classes. If not, here is a reminder: n!, which reads as "n factorial," is defined as
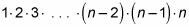
Using the combination formula gives you the following:

Replace all
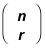
with the coefficients from Step 2.
1(1)8(2i)0 + 8(1)7(2i)1 + 28(1)6(2i)2 + 56(1)5(2i)3 + 70(1)4(2i)4 + 56(1)3(2i)5 + 28(1)2(2i)6 + 8(1)1(2i)7 + 1(1)0(2i)8
Raise the monomials to the powers specified for each term.
1(1)(1) + 8(1)(2i) + 28(1)(4i2) + 56(1)(8i3) + 70(1)(16i4) + 56(1)(32i5) + 28(1)(64i6) + 8(1)(128i7) + 1(1)(256i8)
Simplify any i's that you can.
1(1)(1) + 8(1)(2i) + 28(1)(4)(–1) + 56(1)(8)(–i) + 70(1)(16)(1) + 56(1)(32)(i) + 28(1)(64)(–1) + 8(1)(128)(–i) + 1(1)(256)(1)
Combine like terms and simplify.
1 + 16i – 112 – 448i + 1,120 + 1,792i – 1,792 – 1,024i + 256
= –527 + 336i

