You can evaluate the volume of a solid of revolution. A solid of revolution is created by taking a function, or part of a function, and spinning it around an axis — in most cases, either the x-axis or the y-axis.
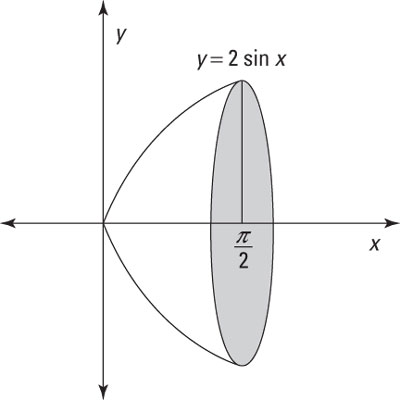
For example, the left side of the figure shows the function y = 2 sin x between x = 0 and
Every solid of revolution has circular cross sections perpendicular to the axis of revolution. When the axis of revolution is the x-axis (or any other line that’s parallel with the x-axis), you can use the meat-slicer method directly.
However, when the axis of revolution is the y-axis (or any other line that’s parallel with the y-axis), you need to modify the problem.
To find the volume of this solid of revolution, use the meat-slicer method:
Find an expression that represents the area of a random cross section of the solid (in terms of x).
This cross section is a circle with a radius of 2 sin x:
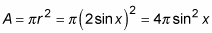
Use this expression to build a definite integral (in terms of dx) that represents the volume of the solid.
This time, the limits of integration are from 0 to π/2:
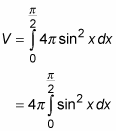
Evaluate this integral by using the half-angle formula for sines:
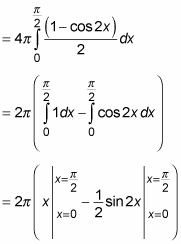
Now evaluate:
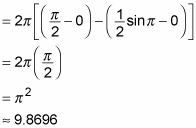
So the volume of this solid of revolution is approximately 9.8696 cubic units.

