An alternating series is a series where the terms alternate between positive and negative. You can say that an alternating series converges if two conditions are met:
Its nth term converges to zero.
Its terms are non-increasing — in other words, each term is either smaller than or the same as its predecessor (ignoring the minus signs).
Using this simple test, you can easily show many alternating series to be convergent. The terms just have to converge to zero and get smaller and smaller (they rarely stay the same). The alternating harmonic series converges by this test:
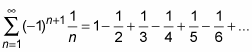
As do the following two series:
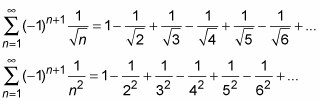
The alternating series test can only tell you that an alternating series itself converges. The test says nothing about the positive-term series. In other words, the test cannot tell you whether a series is absolutely convergent or conditionally convergent. To answer that question, you must investigate the positive series with a different test. (If the alternating series is convergent as it is, it must be either absolutely or conditionally convergent; it’s just that you can’t determine which it is unless you’re able to figure out whether or not the positive-term series converges.)
Now try the following problem. Determine the convergence or divergence of the following series. If convergent, determine whether the convergence is conditional or absolute.
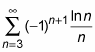
Check that the nth term converges to zero.
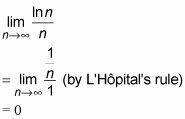
Always check the nth term first because if it doesn’t converge to zero, you’re done — the alternating series and the positive series will both diverge. Note that the nth term test of divergence applies to alternating series as well as positive series.
Check that the terms decrease or stay the same (ignoring the minus signs).

This is negative for all x ≥ 3 (because the natural log of anything 3 or higher is more than 1 and x-squared, of course, is always positive), so the derivative and thus the slope of the function are negative, and therefore the function is decreasing. Finally, because the function is decreasing, the terms of the series are also decreasing. (Recall that ignoring any number of terms at the beginning of a series doesn’t affect whether the series converges or diverges or whether convergence is conditional or absolute; that’s why it’s okay to begin with x = 3 and n = 3.) That does it.
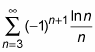
converges by the alternating series test.
Determine the type of convergence.
You can see that for n ≥ 3 the positive series,
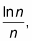
is greater than the divergent harmonic series,
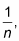
so the positive series diverges by the direct comparison test. Thus, the alternating series is conditionally convergent.
If the alternating series fails to satisfy the second requirement of the alternating series test, it does not follow that your series diverges, only that this test fails to show convergence.

