Pre-Calculus: 1001 Practice Problems For Dummies (+ Free Online Practice)
Explore Book Buy On AmazonThe period of the parent graphs of sine and cosine is 2 multiplied by pi, which is once around the unit circle. Sometimes in trigonometry, the variable x, not the function, gets multiplied by a constant. This action affects the period of the trig function graph.
For example, f(x) = sin 2x makes the graph repeat itself twice in the same amount of time; in other words, the graph moves twice as fast. Think of it like fast-forwarding a DVD. This figure shows function graphs with various period changes.
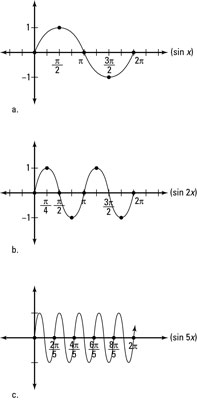
To find the period of f(x) = sin 2x,
and solve for the period. In this case,
Each period of the graph finishes at twice the speed.
You can make the graph of a trig function move faster or slower with different constants:
-
Positive values of period greater than 1 make the graph repeat itself more and more frequently.
You see this rule in the example of f(x).
-
Fraction values between 0 and 1 make the graph repeat itself less frequently.
For example, if
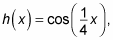
you can find its period by setting
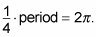
Solving for period gets you
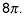
Before, the graph finished at
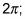
now it waits to finish at
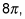
which slows it down by 1/4.
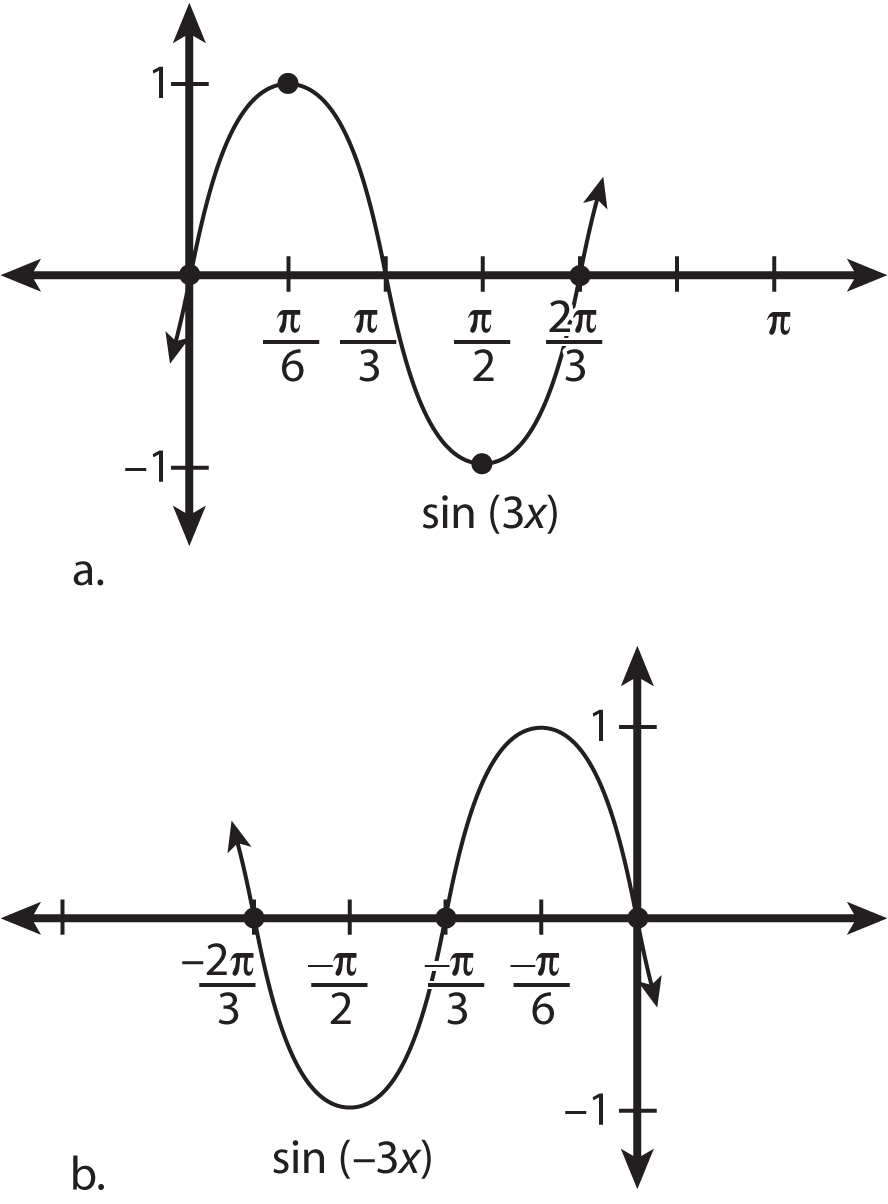
You can have a negative constant multiplying the period. A negative constant affects how fast the graph moves, but in the opposite direction of the positive constant. For example, say p(x) = sin(3x) and q(x) = sin(–3x). The period of p(x) is
whereas the period of q(x) is
The graph of p(x) moves to the right of the y-axis, and the graph of q(x) moves to the left. The figure illustrates this point clearly. Keep in mind that these graphs represent only one period of the function. The graph actually repeats itself in both directions infinitely many times.
Don't confuse amplitude and period when graphing trig functions. For example, f(x) = 2 sin x and g(x) = sin 2x affect the graph differently: f(x) = 2 sin x makes it taller, and g(x) = sin 2x makes it move faster.

