If you don't have the unit circle at your disposal (if you're taking a test, for instance), you can draw a picture and find the values you need the long way.
Sine and cosine
The point-in-the-plane definition of cosine in a right triangle isBecause the hypotenuse r is always 1 in the unit circle, the x value is the cosine value. And if you remember the alternate definition of sine,
you'll realize that the y value is the sine value. Therefore, any point anywhere on the unit circle is always
Talk about putting all the pieces together!
Alphabetically, x comes before y and c comes before s (cosine comes before sine, in other words). This fact should help you remember which one is which.
Tangent, cotangent, secant, and cosecant
Tangent, cotangent, secant, and cosecant require a little more effort than the sine and cosine do. For many angles on the unit circle, evaluating these functions requires some careful work with fractions and square roots.Remember to always rationalize the denominator for any fraction in your final answer. Also, remember that any number divided by 0 is undefined. The tangent and secant functions, for instance, are undefined when the cosine value is 0. Similarly, the cotangent and cosecant values are undefined when the sine value is 0.
Time for an example. To evaluate the six trigonometric functions of 225 degrees using the unit circle, follow these steps:
-
Draw the picture.
When you're asked to find the trig function of an angle, you don't have to draw out a unit circle every time. Instead, use your smarts to figure out the picture. For this example, 225 degrees is 45 degrees more than 180 degrees. Draw out a 45-45-90-degree triangle in the third quadrant only.
-
Fill in the lengths of the legs and the hypotenuse.
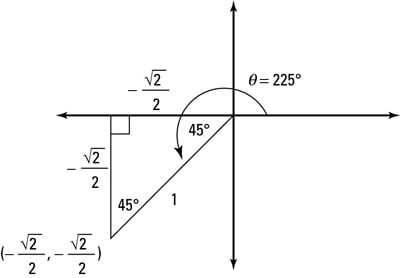 A 45er triangle, decked out like a Christmas tree
A 45er triangle, decked out like a Christmas treeUse the rules of the 45er triangle. The coordinate of the point at 225 degrees is
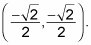
The figure shows the triangle, as well as all the information to evaluate the six trig functions.
Be careful! Use what you know about the positive and negative axes on the coordinate plane to help you. Because the triangle is in the third quadrant, both the x and y values should be negative.
-
Find the sine of the angle.
The sine of an angle is the y value, or the vertical line that extends from the point on the unit circle to the x-axis. For 225 degrees, the y value is
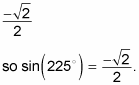
-
Find the cosine of the angle.
The cosine value is the x value, so it must be
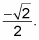
-
Find the tangent of the angle.
To find the tangent of an angle on the unit circle, you use the tangent's alternate definition:
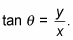
Another way of looking at it is that
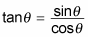
because in the unit circle, the y value is the sine and the x value is the cosine. So if you know the sine and cosine of any angle, you also know the tangent. (Thanks, unit circle!) The sine and the cosine of 225 degrees are both
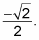
Therefore, you can divide the sine by the cosine to get the tangent of 225 degrees, which is 1.
-
Find the cosecant of the angle.
The cosecant of any angle is
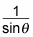
or r/y, using the point-in-the-plane definition. Using what you determined in Step 1,
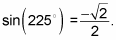
You can now divide 1 by
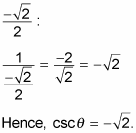
-
Find the secant of the angle.
The secant of any angle is
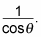
Because the cosine of 225 degrees is also
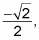
found in Step 4, the secant of 225 degrees is
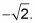
-
Find the cotangent of the angle.
The cotangent of an angle is
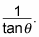
From Step 5, tan (225 degrees) = 1. So cot (225 degrees) = 1/1 = 1. Easy as pie (but not pi, which is another subject entirely).

