A good way to approximate areas with rectangles is to make each rectangle cross the curve at the midpoint of that rectangle's top side. A midpoint sum is a much better estimate of area than either a left-rectangle or right-rectangle sum. The below figure shows why.
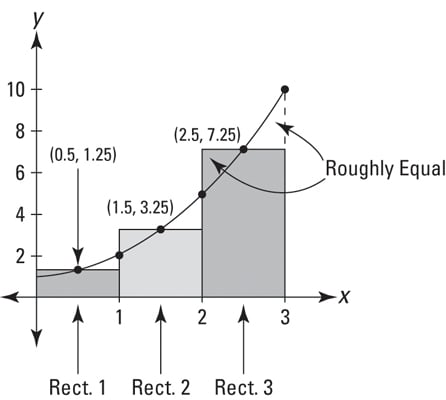
You can see in the figure that the part of each rectangle that’s above the curve looks about the same size as the gap between the rectangle and the curve. A midpoint sum produces such a good estimate because these two errors roughly cancel out each other.
The figure above shows how you’d use three midpoint rectangles to estimate the area under
from 0 to 3. For the three rectangles, their widths are 1 and their heights are f(0.5) = 1.25, f(1.5) = 3.25, and f(2.5) = 7.25. Area = base x height, so add 1.25 + 3.25 + 7.25 to get the total area of 11.75.
Using the definite integral, you find that the exact area under this curve turns out to be 12, so the error with this three-midpoint-rectangles estimate is 0.25. Contrast that with the much worse errors of the three-left-rectangles estimate and the three-right-rectangles estimate of 4.0 and 5.0, respectively.
Here's the official midpoint rule:
Midpoint Rectangle Rule—You can approximate the exact area under a curve between a and b,
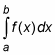
with a sum of midpoint rectangles given by the following formula. In general, the more rectangles, the better the estimate:
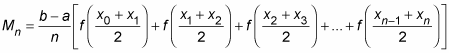
Where, n is the number of rectangles,
is the width of each rectangle, and the function values are the heights of the rectangles.

