You can approximate the area under a curve by summing up “left” rectangles. For example, say you want the area under the curve f (x) = x2 + 1 from 0 to 3. The shaded area of the graph on the left side of the figure below shows the area you want to find.
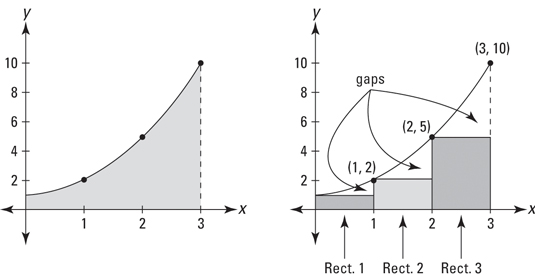
You can get a rough estimate of that area by drawing three rectangles under the curve, as shown in the graph on the right side of the figure, and then determining the sum of their areas. The rectangles in the figure make up a so-called left sum because the upper-left corner of each rectangle touches the curve.
In this example, each rectangle has a width of 1 and the height of each is given by the height of the function at the rectangle’s left edge. So, rectangle number 1 has a height of
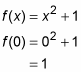
Its area (length x width or height x width) is thus 1 x 1, or 1. Rectangle 2 has a height of
so its area is 2 x 1, or 2. And rectangle 3 has a height of
so its area is 5 x 1, or 5. Adding these three areas gives you a total of 1 + 2 + 5, or 8. You can see that this is an underestimate of the total area under the curve because of the three gaps between the rectangles and the curve shown in the above figure.
For a better estimate, double the number of rectangles to six. The following figure shows six “left” rectangles under the curve and also how the six rectangles begin to fill up the three gaps you see in the first figure.
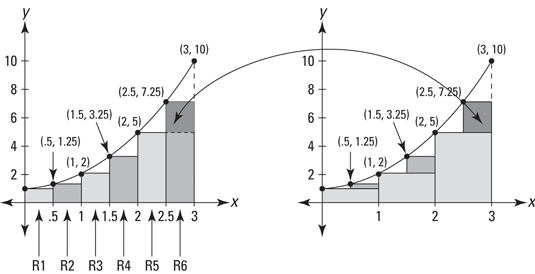
See the three small shaded rectangles in the graph on the right in the second figure? They sit on top of the three rectangles from the first figure, and they represent how much the area estimate has improved by using six rectangles instead of three.
Now total up the areas of the six rectangles. Each has a width of 0.5 and the heights are f(0), f(0.5), f(1), f(1.5), and so on. Here’s the total: 0.5 + 0.625 + 1 + 1.625 + 2.5 + 3.625 = 9.875. This is a better estimate, but it’s still an underestimate because of the six small gaps you can see on the left-side graph in the above figure.
Here’s the fancy-pants formula for a left rectangle sum.
The Left Rectangle Rule: You can approximate the exact area under a curve between a and b,
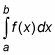
with the sum of left rectangles given by the following formula. In general, the more rectangles, the better the estimate.
Where n is the number of rectangles,
is the width of each rectangle, and the function values are the heights of the rectangles.
Look back to the six rectangles shown in the second figure. The width of each rectangle equals the length of the total span from 0 to 3 (which of course is 3 – 0, or 3) divided by the number of rectangles, 6. That’s what the
does in the formula.
Now, what about those xs with the subscripts? The x-coordinate of the left edge of rectangle 1 in the second figure is called
the right edge of rectangle 1 (which is the same as the left edge of rectangle 2) is at
the right edge of rectangle 2 is at
the right edge of rectangle 3 is at
and so on all the way up to the right edge of rectangle 6, which is at
For the six rectangles in the second figure,
The heights of the six left rectangles in the second figure occur at their left edges, which are at 0, 0.5, 1, 1.5, 2, and 2.5 — that’s
You don’t use the right edge of the last rectangle,
in a left sum. That’s why the list of function values in the formula stops at
Here’s how to use the formula for the six rectangles in the second figure:
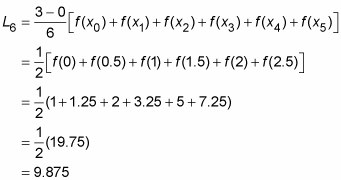
(Note that had you distributed the width of 1/2 to each of the heights after the third line in the above solution, you would have seen the sum of the areas of the six rectangles (like in the sum of numbers two paragraphs below the second figure). The formula immediately above just uses the shortcut of first adding up the heights and then multiplying by the width.)

