Find Concavity and Inflection Points Using Second Derivatives — Practice Questions

One purpose of the second derivative is to analyze concavity and points of inflection on a graph. The following figure shows a graph with concavity and two points of inflection.

Concavity and points of inflection.

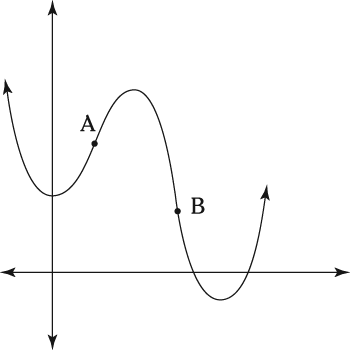
Using this figure, here are some points to remember about concavity and inflection points:

• The section of curve between A and B is concave down — like an upside-down spoon or a frown; the sections on the outsides of A and B are concave up — like a right-side up spoon or a smile; and A and B are inflection points.

• A positive second derivative means that section is concave up, while a negative second derivative means concave down. And where the concavity switches from up to down or down to up (like at A and B), you have an inflection point, and the second derivative there will (usually) be zero.

Practice questions

1. Find the intervals of concavity and the inflection points of f(x) = –2x³ + 6x² – 10x + 5.

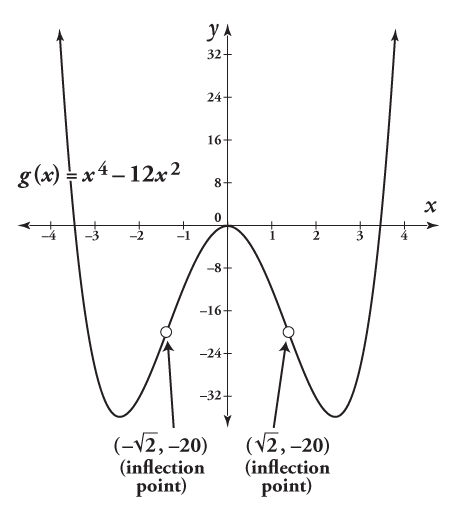
2. Find the intervals of concavity and the inflection points of g(x) = x⁴ – 12x².

Answers and explanations

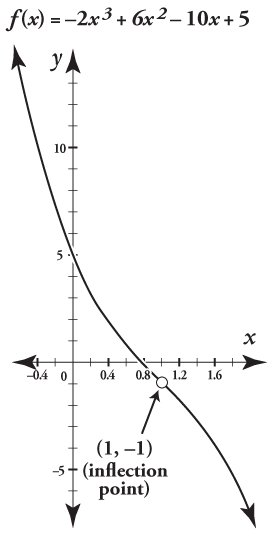
1. For f(x) = –2x³ + 6x² – 10x + 5, f is concave up from negative infinity to the inflection point at (1, –1), then concave down from there to infinity.

   

   To solve this problem, start by finding the second derivative.

   

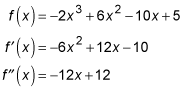
   Now set it equal to 0 and solve.

   

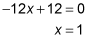
   Check for x values where the second derivative is undefined. (There are none.)

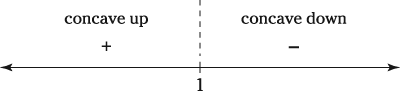
   Now test your two regions, to the left and to the right of x = 1.

   

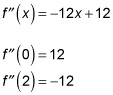
   Make a sign graph, as shown here.

   

   Because the concavity switches at x = 1 and because

   

   equals zero there, there's an inflection point at x = 1.

   Find the height of the inflection point.

   

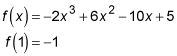
   Thus f is concave up from negative infinity to the inflection point at (1, –1), and then concave down from there to infinity. As always, you should check your result on your graphing calculator. Hint: To get a good feel for the look of this function, you need a fairly odd graphing window — try something like xmin = –2, xmax = 4, ymin = –20, ymax = 20.

2. For g(x) = x⁴ – 12x², g is concave up from negative infinity to the inflection point at

   

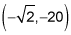
   then concave down to an inflection point at

   

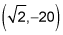
   then concave up again to infinity.

   

   To solve this problem, start by finding the second derivative.

   

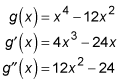
   Now set it to 0 and solve.

   

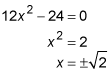
   Is the second derivative undefined anywhere? No.

   Now it's time to test the three regions.

   

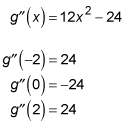
   Make a sign graph, as shown here.

   

   Because the concavity switched signs at the two zeros of

   

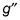
   there are inflection points at these two x values.

   Find the heights of the inflection points.

   

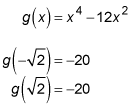
   g is concave up from negative infinity to the inflection point at

   

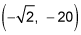
   concave down from there to another inflection point at

   

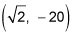
   and then concave up again from there to infinity.