Have you ever looked at a distant horizon and wondered just how far away it was? Wonder no more! Now, you can use differentiation to solve this age-old problem.
Before you get started, though, take a moment to refresh your memory on tangents and normals:
At its point of tangency, a tangent line has the same slope as the curve it's tangent to. In calculus, whenever a problem involves slope, you should immediately think derivative. The derivative is the key to all tangent line problems.
At its point of intersection to a curve, a normal line is perpendicular to the tangent line drawn at that same point. When any problem involves perpendicular lines, you use the rule that perpendicular lines have slopes that are opposite reciprocals. So all you do is use the derivative to get the slope of the tangent line, and then the opposite reciprocal of that gives you the slope of the normal line.
Practice question
The Earth has a radius of 4,000 miles. Say you're standing on the shore and your eyes are 5 feet, 3.36 inches above the surface of the water. How far out can you see to the horizon before the Earth's curvature makes the water dip below the horizon? (Refer to the following figure.)
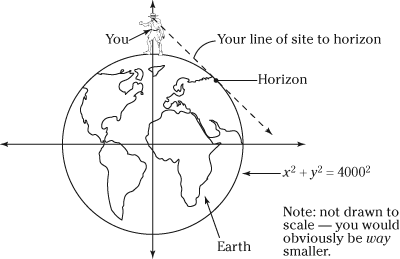
Answer and explanation
The horizon is about 2.83 miles away.
How do you get that? First, write the equation of the Earth's circumference as a function of y.
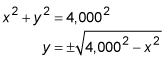
You can disregard the negative half of this circle because your line of sight will obviously be tangent to the upper half of the Earth.
Now, express a point on the circle in terms of x:
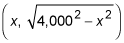
Take the derivative of the circle.
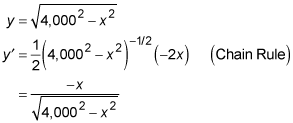
Using the slope formula, set the slope of the tangent line from your eyes to
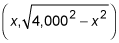
equal to the derivative and then solve for x.
Your eyes are
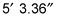
above the top of the Earth at the point (0, 4,000) on the circle. Convert your height to miles; that's exactly 0.001 miles (what an amazing coincidence!). So the coordinates of your eyes are (0, 4,000.001).

Many people are surprised that the horizon is so close. What do you think?

