If you traveled from point A to point B at an average speed of, say, 50 mph, then according to the Mean Value Theorem, there would be at least one point during your trip when your speed was exactly 50 mph.
In more technical terms, with the Mean Value Theorem, you can figure the average rate or slope over an interval and then use the first derivative to find one or more points in the interval where the instantaneous rate or slope equals the average rate or slope.
The following practice questions ask you to find values that satisfy the Mean Value Theorem in a given interval.
Practice questions
For g(x) = x3 + x2 – x, find all the values c in the interval (–2, 1) that satisfy the Mean Value Theorem.
For s(t) = t4/3 – 3t1/3, find all the values c in the interval (0, 3) that satisfy the Mean Value Theorem.
Answers and explanations
The values of c are
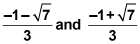
To find these values, you start by finding the first derivative.
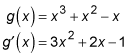
Then you figure the slope between the endpoints of the interval.
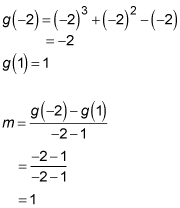
Finally, you set the derivative equal to this slope and solve.
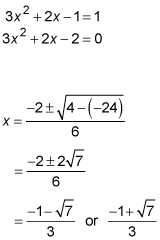
Both are inside the given interval, so you have two answers.
The value of c is
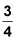
To find this value, you start by finding the first derivative.
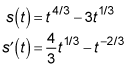
Then, you figure the slope between the endpoints of the interval.
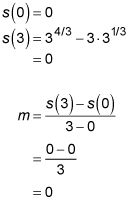
Finally, you set the derivative equal to the slope and solve.
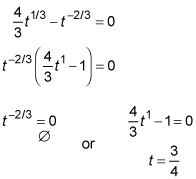
Graph s to confirm that its slope at
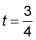
is zero.

