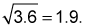Moments are summary measures of a probability distribution, and include the expected value, variance, and standard deviation. The expected value represents the mean or average value of a distribution. The expected value is sometimes known as the first moment of a probability distribution. You calculate the expected value by taking each possible value of the distribution, weighting it by its probability, and then summing the results. The expected value is comparable to the mean of a population or sample.
The variance and standard deviation represent the dispersion among the possible values of a probability distribution. The variance and standard deviation of a probability distribution are equivalent to the variance and standard deviation of a population or sample. The variance is sometimes known as the second central moment of a probability distribution; the standard deviation isn't a separate moment, but simply the square root of the variance.
Luckily, for the binomial distribution, you can reduce computation time by using a series of simplified formulas.
How to calculate the expected value of the binomial distribution
The expected value of a probability distribution is its average value. You get it by weighing each possible value by its probability of occurring. For the binomial distribution, the calculation of the expected value can be simplified to
E(X) = np
For example, suppose that 10 percent of all people are left-handed, and 90 percent are right-handed (which happens to be true). In a class of 40 students, what's the expected number of left-handed students? You can calculate the expected value by thinking of each student as a "trial," with a 10 percent chance of being left-handed (a "success") and 90 percent chance of being right-handed (a "failure"). Therefore, n = 40 and p = 0.10. The expected number of left-handed students in the class is E(X) = np = (40)(0.10) = 4.
How to compute the variance and standard deviation of the binomial distribution
The variance of a distribution is the average squared distance between each possible outcome and the expected value. For the binomial distribution, you may compute the variance with the following simplified formula:
The standard deviation of a distribution equals the square root of the variance. For the binomial distribution, you calculate the standard deviation as
For the example of left-handed students,
The expected value is E(X) = np = (40)(0.10) = 4.
The variance is
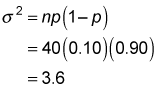
The standard deviation is