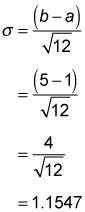The uniform distribution is used to describe a situation where all possible outcomes of a random experiment are equally likely to occur. You can use the variance and standard deviation to measure the "spread" among the possible values of the probability distribution of a random variable.
For example, suppose that an art gallery sells two types of art work: inexpensive prints and original paintings. The length of time that the prints remain in inventory is uniformly distributed over the interval (0, 40). For example, some prints are sold immediately; no print remains in inventory for more than 40 days. For the paintings, the length of time in inventory is uniformly distributed over the interval (5, 105). For example, each painting requires at least 5 days to be sold and may take up to 105 days to be sold.
The variance and the standard deviation measure the degree of dispersion (spread) among the values of a probability distribution. In the art gallery example, the inventory times of the prints are much closer to each other than for the paintings. As a result, the variance and standard deviation are much lower for the prints because the range of possible values is much smaller.
For the uniform distribution defined over the interval from a to b, the variance equals
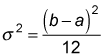
The standard deviation is the square root of the variance:
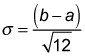
For example, the variance of the uniform distribution defined over the interval (1, 5) is computed as follows:
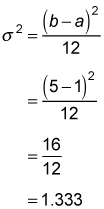
The standard deviation is: