A solution of a system of two linear equations consists of the values of x and y that make both of the equations true — at the same time. Graphically, the solution is the point where the two lines intersect. The two most frequently used methods for solving systems of linear equations are elimination and substitution:
Elimination (also called add-subtract): This method involves adding the two equations together — or multiples of the two equations — so that in the sum, the coefficient of one of the variables becomes 0. That variable drops out (is eliminated), so you can solve for the other variable. Then you plug the solution back into one of the original equations and solve for the variable you eliminated.
Substitution: This method has you set one of the equations equal to x or y. You can then substitute the equivalent of the variable from one equation for that variable into the other equation. You end up with a single-variable equation, which you can solve. Then plug that answer into one of the original equations and solve for the other variable.
You can use either method to solve linear systems, and you choose one over the other if a method seems to work better in a particular system (substitution works best if the coefficient on one of the variables is 1 or –1). The following examples show the same system of equations solved using both methods.
Sample questions
Use elimination to solve for the common solution in the two equations: x + 3y = 4 and 2x + 5y = 5.
x= –5, y= 3. Multiply each term in the first equation by –2 (you get –2x – 6y = –8) and then add the terms in the two equations together.
You choose the number –2 as a multiplier because it makes the coefficient of the x term in the first equation equal to –2, while the coefficient on x in the second equation is 2. The numbers –2 and 2 are opposites, so adding the equations together eliminates the x term:
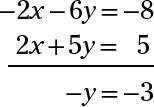
Now solve –y = –3 for y, and you get y = 3. Put 3 in for y in the first original equation, and you have x + 3(3) = 4; x + 9 = 4; x = –5. The solution is x = –5, y = 3, also written as the ordered pair (–5, 3). You can also solve for the x-value by putting the 3 into the second equation — you get the same result.
Use substitution to solve for the common solution in the two equations: x + 3y = 4 and 2x + 5y = 5.
x = –5, y = 3.To use substitution, select a variable in one of the equations with a coefficient of 1 or –1. The only variable that qualifies in this system is x in the first equation. Solve for x in terms of y in that equation. You get x = 4 – 3y.
Substitute that equivalent of x into the second equation. The second equation becomes 2(4 – 3y) + 5y = 5. Solve that equation for y: 8 – 6y + 5y = 5; 8 – y = 5; –y = –3; y = 3. That answer should look familiar. Substitute the 3 into x + 3y = 4 to get x: x + 3(3) = 4; x + 9 = 4; x = –5.
Practice questions
Solve for the common solution in the two equations: 5x – 3y = 7 and 2x + 3y = 7.
Solve for the common solution in the two equations: 8x – 3y = 41 and 3x + 2y = 6.
Solve for the common solution in the two equations: 4x + 5y = 11 and y = 2x + 5.
Following are answers to the practice questions:
The answer is x= 2, y = 1.
The coefficients of the y terms are opposites of one another, so when you add the two equations together, you get 7x = 14; x = 2. Replace the x with 2 in the first equation: 5(2) – 3y = 7; 10 – 3y = 7, –3y = –3; y = 1.
The answer is x= 4, y = –3.
Multiply the terms in the first equation by 2 and the terms in the second equation by 3. As a result, you end up adding –6y and 6y together, which eliminates the y terms when you add the two equations. You get 25x = 100; x = 4. Replace the x with 4 in the second equation: 3(4) + 2y = 6; 12 + 2y = 6; 2y = –6; y = –3.
The answer is x= –1, y = 3.
The second equation is already solved for y. Substitute the equivalent of y from the second equation into the first equation to get 4x + 5(2x + 5) = 11. Distribute and simplify: 4x + 10x + 25 = 11; 14x + 25 = 11; 14x = –14; x = –1. Replace the x with –1 in the second equation: y = 2(–1) + 5 = 3.

