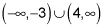In algebra, solving a quadratic inequality is very similar to solving a quadratic equation. The difference is that with quadratic equations, you set the expressions equal to zero, but with inequalities, you're interested in what's on either side of the zero (positives and negatives).
To solve a quadratic inequality, you follow these steps:
Move all the terms to one side of the inequality sign.
Factor, if possible.
Determine all zeros (roots, or solutions).
Zeros are the values of the variable that make each factored expression equal to zero.
Put the zeros in order on a number line.
Create a sign line to show where the expression in the inequality is positive or negative.
A sign line shows the signs of the different factors in each interval. If the expression is factored, show the signs of the individual factors.
Determine the solution, writing it in inequality notation or interval notation.
Here's an example: Solve the inequality x2 – x > 12.
Here, you need to determine what values of x you can square so that when you subtract the original number, your answer will be bigger than 12.
Follow the steps:
Subtract 12 from each side of the inequality x2 – x > 12 to move all the terms to one side.
You end up with x2 – x – 12 > 0.
Factoring on the left side of the inequality, you get (x – 4)(x + 3) > 0.
Determine that all the zeroes for the inequality are x = 4 and x = –3.
Put the zeros in order on a number line, shown in the following figure.

Create a sign line to show the signs of the different factors in each interval.
Between –3 and 4, try letting x = 0 (you can use any number between –3 and 4). When x = 0, the factor (x – 4) is negative, and the factor (x + 3) is positive. Put those signs on the sign line to correspond to the factors. Do the same for the interval of numbers to the left of –3 and to the right of 4 (see the next illustration).
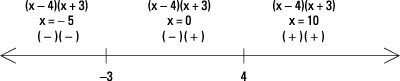
Keep in mind that the x values in each interval are really random choices (as you can see from the choices in this example of x = –5 and x = 10). Any number in each of the intervals gives you the same positive or negative value to the factor.
To determine the solution, look at the signs of the factors; you want the expression to be positive, corresponding to the inequality greater than zero.
The interval to the left of –3 has a negative times a negative, which is positive. So, any number to the left of –3 works. You can write that part of the solution as x < –3 or, in interval notation,
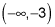
The interval to the right of 4 has a positive times a positive, which is positive. So, x > 4 is a solution; you can write it as
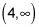
The interval between –3 and 4 is always negative; you have a negative times a positive. The complete solution lists both intervals that have working values in the inequality.
The solution of the inequality x2 – x > 12, therefore, is x < –3 or x > 4. Writing this result in interval notation, you replace the word "or" with the symbol
and write it as