Of the four types of conic sections, the hyperbola is the only conic that seems a bit disconnected. The graph of a hyperbola is two separate curves seeming to face away from one another. The standard forms for the equation of hyperbolas are
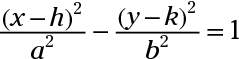
or
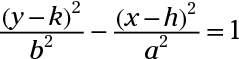
Notice that these formulas look just like the equation for the ellipse except for the minus sign between the two fractions.
Two forms of the standard equation exist; the form with the x-term in front is for hyperbolas that open to the left and right, and the form with the y-term in front is for hyperbolas that open upward and downward. The center of the hyperbola is the same old (h, k), as in the circles and ellipses.
You measure distances from the foci of a hyperbola to a point on the hyperbola. The difference between the distances (in the ellipse it’s the sum) is always the same for any point on the hyperbola.
Solve for the foci with c2 = a2 + b2, and let +/– c be the distance from the center to the foci, either vertically or horizontally (depending on the equation, which tells you whether the hyperbola opens up and down or left and right).
Sample questions
Find the standard form of the hyperbola 16x2 – 9y2 = 144. Then give the coordinates of the center and the coordinates of the foci.
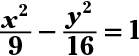
center: (0, 0); foci: (–5, 0), (5, 0). Divide each side of the equation by 144, and you get the standard form. The hyperbola opens left and right, because the x term appears first in the standard form. The center of the hyperbola is (0, 0), the origin.
To find the foci, solve for c with c2 = a2 + b2 = 9 + 16 = 25. The value of c is +/– 5. Counting 5 units to the left and right of the center, the coordinates of the foci are (–5, 0) and (5, 0).
Find the standard form of the hyperbola 576(y – 5)2 – 49(x – 3)2 = 28,224. Then give the coordinates of the center and the coordinates of the foci.
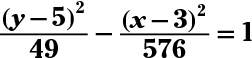
center: (3, 5); foci: (3, 30), (3, –20). Divide each side of the equation by 28,224 (yes, the number is huge, but the fractions reduce very nicely) to get the standard form. The hyperbola opens upward and downward, because the y term appears first in the standard form. The center of the hyperbola is (3, 5).
To find the foci, solve for c with c2 = a2 + b2 = 49 + 576 = 625. The value of c is +/– 25. Counting 25 units upward and downward from the center, the coordinates of the foci are (3, 30) and (3, –20).
Practice questions
Find the standard form of the hyperbola 3x2 – 18y2 = 18. Then give the coordinates of the center and the coordinates of the foci.
Find the standard form of the hyperbola 25y2 – 144x2 = 3,600. Then give the coordinates of the center and the coordinates of the foci.
Following are answers to the practice questions:
The answer is equation:
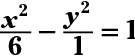
center: (0, 0); foci:
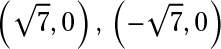
Divide each term by 18 to get the standard form. The hyperbola opens left and right, because the x term appears first in the standard form. Solving c2 = 6 + 1 = 7, you find that
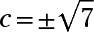
Add and subtract c to and from the x-coordinate of the center to get the coordinates of the foci.
The answer is equation:
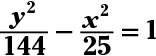
center: (0, 0); foci: (0, 13), (0, –13).
Divide each term by 3,600 to get the standard form. The hyperbola opens upward and downward, because the y term appears first in the standard form. Solving c2 = 144 + 25 = 169, you find that c = +/– 13. Add and subtract c to and from the y-coordinate of the center to get the coordinates of the foci.

