You can describe the elements in a set in several different ways, but you usually want to choose the method that’s quickest and most efficient and/or clearest to the reader. The two main methods for describing a set are roster and rule (or set-builder).
A roster is a list of the elements in a set. When the set doesn’t include many elements, then this description works fine. If the set contains a lot of elements, you can use an ellipsis ( . . . ) if the pattern is obvious (a nasty word in mathematics). A rule works well when you find lots and lots of elements in the set.
Sample questions
Use roster and rule notation to describe the set F, which consists of all the positive multiples of 5 that are less than 50.
Roster notation: F = {5, 10, 15, 20, 25, 30, 35, 40, 45}; rule notation:
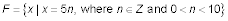
You read the rule as “Set F consists of all x’s such that x is equal to five times n, where n is an integer and n is a number between zero and ten.”
The symbol Z stands for integers. Of course, you don’t have to write the elements in the set in order. You can just as easily write F = {10, 20, 30, 40, 45, 35, 25, 15, 5}.
Write the elements of set C in roster form if C = {x | x = a2 and x = b3, where 0 < a, b < 30}.
C= {1, 64, 729}. The rule for C is that x has to be a perfect square and a perfect cube. The bases of x (a and b) are positive numbers less than 30.
The best way to approach this problem is to find all the squares of the numbers from 1 to 30 and then determine which are cubes: C = {1, 64, 729}. You get these elements because 1 = 12 = 13, 64 = 82 = 43, and 729 = 272 = 93.
Practice questions
Write set A using roster notation if A = {x | x is odd, x = 7n, 0 < x < 70}.
Write set C using a rule if C = {11, 21, 31, 41, 51, 61}.
Write set D using a rule if D = {1, 5, 9, 13, 17, 21, … }.
Following are answers to the practice questions:
Write set A using roster notation if A = {x | x is odd, x = 7n, 0 < x < 70}. The answer is {7, 21, 35, 49, 63}.
According to the rule, you want numbers that are odd, multiples of 7, and between 0 and 70.
Write set C using a rule if C = {11, 21, 31, 41, 51, 61}. The answer is
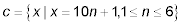
Another way of writing the rule is
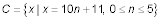
Notice that in this second rule, the values of n are different — they begin and end in different places — and the constant 11 is different. What’s alike in these two rules is that the n is multiplied by 10, keeping the terms 10 units apart.
Write set D using a rule if D = {1, 5, 9, 13, 17, 21, … }. The answer is
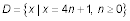
The rule allows the set to be infinite — the number of terms has no end.

