In algebra, a one-sided limit tells you what a function is doing at an x-value as the function approaches from one side or the other. One-sided limits are restrictive, and work only from the left or from the right.
When a rational function doesn't have a limit at a particular value, the function values and graph have to go somewhere. A particular function may not have the number 3 in its domain, and its graph may have a vertical asymptote when x = 3. Even though the function has no limit, you can still say something about what's happening to the function as it approaches 3 from the left and the right. The graph has no numerical limit at that point, but you can still tell something about the behavior of the function. The behavior is attributed to one-sided limits.
The notation for indicating one-sided limits from the left or right is shown here:
The limit as x approaches the value a from the left is
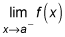
The limit as x approaches the value a from the right is
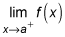
Do you see the little positive or negative sign after the a? You can think of from the left as coming from the same direction as all the negative numbers on the number line and from the right as coming from the same direction as all the positive numbers.
The table shows some values of the function
which has a vertical asymptote at x = 3.
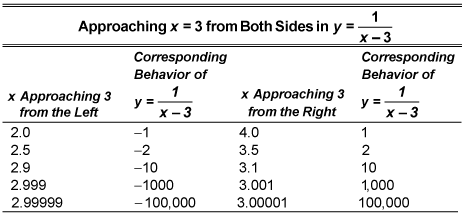
You express the one-sided limits for the function from the table as follows:
The function goes down to negative infinity as it approaches 3 from less than the value and up to positive infinity as it approaches 3 from greater than the value. "And nary the twain shall meet."

