Evaluating e-Expressions and Powers of e

When mathematicians and scientists assigned the letter e to represent the number 2.71828 . . . , little did they know that there’d be e-mail, eBay, eMall, and so on. Look what they started!

In the world of mathematics, the letter e is a constant value — slightly smaller than the number 3. The more frequently used exponential and logarithmic functions are based on the constant e, although people use other bases on occasion. The exponential rules apply for all the constant bases.

Here’s a quick review of the rules you need:

b^x x b^y = b^x+y

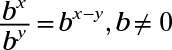
(b^x)^y= b^xy

b⁰ = 1

Sample questions

1. Given the exponential function f(x) = 5^x+1, determine f(–1), f(0), and f(2).

   f(–1) = 1; f(0) = 5; f(2) = 125. Substituting the input value for x in each case, f(–1) = 5^–1+1 = 5⁰ = 1, f(0) = 5⁰⁺¹ = 5¹ = 5, and f(2) = 5²⁺¹ = 5³ = 125.

2. Given the exponential function f(x) = xe^x+1, determine f(–1), f(0), and f(2).

   f(–1) = –1; f(0) = 0; f(2) = 2e³. Substituting the input value for x in each case, f(–1) = –1e^–1+1 = –1 x e⁰ = –1 x 1 = –1, f(0) = 0 x e⁰⁺¹ = 0 x e¹ = 0, and f(2) = 2 x·e²⁺¹ = 2e³. You usually leave powers of e just as they are; don’t bother finding a decimal approximation.

Practice questions

1. Given the exponential function f(x) = 2^x–1, determine f(0), f(1), and f(2).

2. Given the exponential function f(x) =3^x(1 – 2 · 3^x), determine f(0), f(1), and f(2).

3. Given the exponential function f(x) = e^x – 2e^2x, determine f(0) and f(1).

4. Given the exponential function f(x) = (e^x + 2)² – (e^x – 2)², determine f(0), f(1), and f(2).

5. Given the exponential function f(x) = 2(e^x +1)², determine f(0), f(1), and f(–1).

6. Given the exponential function f(x) = x^e– e^x, determine f(0), f(1), and f(2).

Following are answers to the practice questions:

1. The answer is

   

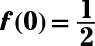
   f(1) = 1; f(2) = 2. Replacing the x’s with the input values, you get

   

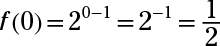
   f(1) = 2^1–1 = 2⁰ = 1, and f(2) = 2^2–1 = 2¹ = 2.

2. The answer is f(0) = –1;f(1) = –15; f(2) = –153.

   Replacing the x’s with the input values, you get f(0) = 3⁰(1 – 2 x 3⁰) = 1(1 – 2) = 1(–1) = –1, f(1) = 3¹(1 – 2 x 3¹) = 3(1 – 6) = 3(–5) = –15, and f(2) = 3²(1 – 2 x 3²) = 9(1 – 2 x 9) = 9(1 – 18) = 9(–17) = –153.

3. The answer is f(0) = –1; f(1) =e– 2e².

   Replacing the x’s with input values, you get f(0) = e⁰ – 2e²⁽⁰⁾ = 1 – 2(1) = –1 and f(1) = e¹ – 2e²⁽¹⁾ = e – 2e².

4. The answer is f(0) = 8; f(1) = 8e; f(2) = 8e².

   Replacing the x’s with input values, you have f(0) = (e⁰ + 2)² – (e⁰ – 2)² = (1 + 2)² – (1 – 2)² = 9 – 1 = 8. For f(1), you get (e¹ + 2)² – (e¹ – 2)². Now expand each binomial and simplify: (e² + 4e + 4) – (e² – 4e + 4) = e² + 4e + 4 – e² + 4e – 4 = 8e.

   Instead of squaring the binomials and simplifying, you can factor the expression as the difference of two squares.

   The difference of two squares factors into the difference and sum of the roots: a² – b² = (a – b)(a + b).

   Here, f(2) = (e² + 2)² – (e² – 2)² = [(e² + 2) – (e² – 2)][(e² + 2) + (e² – 2)] = [e² + 2 – e² + 2][e² + 2 + e² – 2] = [4][2e²] = 8e².

5. The answer is f(0) = 2e²; f(1) = 2e⁴;f(–1) = 2.

   Replacing the x’s with input values, you get f(0) = 2(e⁰⁺¹)² = 2(e¹)² = 2e², f(1) = 2(e^{1 + 1})² = 2(e²)² = 2e⁴, and f(–1) = 2(e^{–1 + 1})² = 2(e⁰)² = 2(1)² = 2.

6. The answer is f(0) = –1;f(1) = 1 –e;

   

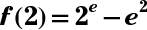
   Replacing the x’s with input values, you get f(0) = 0^e – e⁰ = 0 – 1 = –1, f(1) = 1^e– e¹ = 1 – e, and f(2) = 2^e– e².