Here are a few alphabet functions, called that because they are named using letters from the Greek alphabet. In algebra, a function is a rule or relation that is defined using various mathematical operators. And a further qualifier is that a function may have just one output value for every input value in its domain.
For example, the function f (x) = x2 + 2x – 3 has f (3) = 12 and f (–4) = 5. Every time you input a number for the x, you get one and only one result for that number. This is special, and it’s what makes f (x) a function.
Mathematics is full of many recognizable functions: linear functions, quadratic functions, polynomial functions, exponential functions, logarithmic functions, sine functions, hyperbolic functions, and so on. But there are also many, many functions that are used in mathematics, statistics, physics, and other sciences.
Sigma function
The sigma function is used when studying number theory and other applications where you need to count the divisors of an integer.
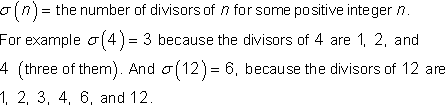
There are all sorts of interesting patterns and theorems involving the sigma function. One of the quickest and easiest patterns or rules to explain is
where p is a prime number. All prime numbers have just two divisors. So
and so on, for all prime numbers.
Gamma function
The gamma function is related to the factorial function, but it can actually do more. Recall that n! is the product of all the positive integers up to and including n. So if f (n) = n!, then
This is a wonderful function and is most useful in probability and statistical applications. However, the input values of f have to be positive integers. The gamma function allows input of real and complex numbers except for the negative integers and 0. The gamma function is
A piece of cake! Just to give you a sampling of some gamma function results:
Delta function
The delta function, or Kronecker delta function, is found naturally in many applications of engineering, physics, and mathematics. This function requires two inputs, i and j, and is defined by a piecewise expression:
So
All functions should be so easy to compute!
Eta function
The eta function, or Dirichlet eta function, is defined by an alternating series and is computed with the following:
So, when s = 4, you have
which converges to a number close to 0.947.
Omega function
The omega function is close in definition to the sigma function. Where the sigma function counts all the divisors of an integer, the omega function counts just the prime factors. There are two versions of the omega function: the simple omega function and the big omega function.
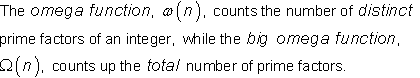
For example,
It has three distinct prime factors and a total of 5 prime factors. So
Pi function
The pi function is also known as the prime counting function. It indicates how many prime numbers are less than the input value. So
because four primes are smaller than 10: 2, 3, 5, and 7. And
because 25 prime numbers are smaller than 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.
Mu function
The mu function, or Möbius function, is important in number theory and combinatorics. It’s another piecewise function, assigning function values based on the prime factors of a particular integer that’s input. Here’s the rule:

Consider the numbers 6, 30, and 18. The factorizations of the numbers are
6 = 2·3, 30 = 2·3·5, and 18 = 2·32.
The number 6 has no squared prime factors and an even number of prime factors. The number 30 has no squared prime factors and an odd number of prime factors. And the number 18 has the squared factor 32. So

