A sequence is a list of terms that has a formula or pattern for determining the numbers to come. A series is the sum of the terms in a sequence. Many sequences of numbers are used in financial and scientific formulas, and being able to add them up is essential.
Adding positive integers
The positive integers are 1, 2, 3, 4, 5, . . . , going on forever. Find the sum of the first n terms of this sequence using this formula:

So, if you want the sum of the first 100 integers, you do the following calculation:
Summing up the squares
The squares of the positive integers are 1, 4, 9, 16, 25, . . . , n2. To find a particular term in this sequence, you just take the square of the number of the term (the 12th term is 122 = 144).
Find the sum of the first n terms using

To add up the numbers 1 + 4 + 9 + 16 + 25 + · · · + 144, you want the sum of the first 12 squares. Using the formula,
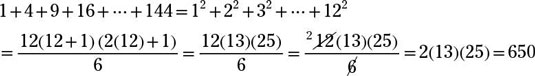
Finding the sum of the cubes
The cubes of the positive integers are 1, 8, 27, 64, 125, . . . , n3. The rule for the general term is n3; you just raise the number of the term to the third power. You can find the sum of these cubes, 13, 23, 33, and so on, using
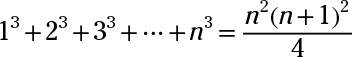
If you look closely, you can see that this formula is just the square of the formula used to find the sum of the first n integers — each factor in the formula is squared.
If you want to find the sum of 1 + 8 + 27 + 64 + 125 + 216 + · · · + 3,375, you first have to figure out whose cube 3,375 is. A simple calculator can find this answer for you. Or, with some sleuthing, you may determine that the root has to end in a 5 for the cube to end in a 5. Seeing that 3,375 = 153 doesn’t take long. Here’s how you find the sum:
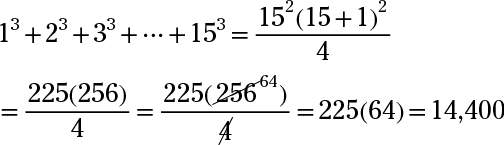
Summing odd numbers
The odd positive integers are 1, 3, 5, 7, 9, . . . , (2n – 1). If you want the fifth odd number, the 9, you replace the n with 5 in 2n – 1 and get 10 – 1 = 9.
When the numbers get large, the process for finding out where a particular odd number falls in the sequence becomes even more important — you really don’t want to have to add up all the numbers for the series, but you have to know how many terms are in the list.
You can calculate, for instance, that the number 2,357 is the 1,179th odd number. You find this answer by solving 2n – 1 = 2,357 and 2n = 2,358. Dividing by 2, you get n = 1,179, so 2,357 is the 1,179th odd number.
The formula for the sum of n odd numbers is 1 + 3 + 5 + · · · + (2n – 1) = n2. To add up the odd numbers 1 + 3 + 5 + 7 + · · · + 2,357, you first determine how many numbers are in the list: 2n – 1 = 2,357, so n = 1,179. The sum is 1,1792 = 1,390,041.
Adding up even numbers
The even positive integers are 2, 4, 6, 8, . . . , 2n. Determine the sum of the first n even numbers with the formula 2 + 4 + 6 + 8 + · · · + 2n = n(n + 1). You may notice that this formula looks somewhat like the formula for adding up the first n integers. Multiply that other formula by 2, and you get the formula for the evens.
Adding up the numbers 2 + 4 + 6 + 8 + · · · + 500, you determine that n = 250. So the sum is 500(501) = 250,500.

