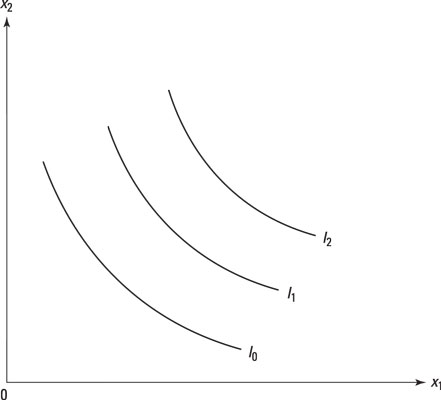
Suppose that you want to compare bundles that are on different levels of utility. Easy! You draw a set of indifference curves moving away from the origin. Each individual curve has the same level of utility along the curves, and each curve expresses a higher level of utility the further away from the origin it is!
The great thing about this depiction is that if you connect a line going through the indifference curves, and the indifference curves are derived from well-behaved preferences, any point on the new line is part of a nice, well-behaved utility function. The following figure shows this, where the new line goes from the origin through the indifference curves.
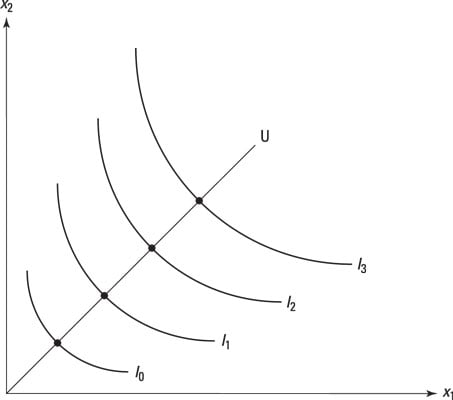
But, you may ask, what if all those points are different combinations of goods? After all, imagine that you've shown that for indifference curve 1, Bob will be indifferent between the bundle of three cups of tea and four cups of coffee and the bundle of five cups of tea and two cups of coffee, but prefers the bundle on indifference curve 2 of six cups of tea and two cups of coffee. What is this telling you?
The answer is something very important about utility functions, which is that if preferences are well-behaved, almost anything that satisfies those rules could be part of a utility function! (In fact, a near infinite number of possible, consistent, utility functions could satisfy those rules. You just wouldn't know which particular one any individual consumer is on until his behavior reveals it in some way.)
The absolutely crucial point to take away is that well-behaved preferences make well-behaved utility functions.

