An important piece of managerial economics, technological change alters the firm’s production function by either changing the relationship between inputs and output or introducing a new product and therefore a new production function. An improvement in technology enables your firm to produce a given quantity of output with fewer inputs shifting the production isoquant inward.
This improvement in technology could be a new production technique, or it could result from organizational changes and improvements in management.
Technological change that introduces new products are difficult to view as a shift in the production function. The new product simply has a new production function. When they were first introduced, there weren’t any goods comparable to computers, mircrowave ovens, and cellular telephones. When introduced, these new goods had their own, new production function.
Technological change has three components — invention, innovation, and diffusion.
Invention refers to a new device, method, or process developed from study and experimentation. According to the United States Patent and Trademark Office, an invention is “any art or process (way of doing or making things), machine manufacture, design, or composition of matter, or any new and useful improvement thereof, or any variety of plant, which is or may be patentable under the patent laws of the United States.”
These definitions of invention exclude an important point. For business success, inventions must be economically viable — in other words, profitable.
An innovation is an invention that’s applied for the first time. Although substantial evaluation occurs during the research and development process, innovation still entails a substantial degree of uncertainty regarding its profitability. This uncertainty can be removed only with the actual implementation of the innovation. After the innovation has been applied, reevaluation occurs based upon additional information obtained.
The two types of innovations are product innovations and process innovations.
Product innovation refers to the introduction of new and improved goods. For many, Wikipedia represents an improvement on printed encyclopedias. Both provide general information but Wikipedia makes it easier — and less costly — for many people to access that information.
Process innovation refers to the introduction of new and improved production processes. Typically, process innovations enable you to manufacture a product more cheaply. Thus, process innovations focus on how things are done. An example of a process innovation is Henry Ford’s introduction of the assembly line in automobile production.
Diffusion examines the speed at which an innovation is adopted. Diffusion seeks to explain how, why, and at what rate innovations are adopted. As a result, diffusion introduces a time element in your decision-making.
How to measure labor productivity
Determining the impact technological change has on your firm is important. Therefore, measuring technological change’s impact is necessary. Two such measures, labor productivity and total factor productivity, are based upon a comparison between the quantity of output produced and the amount of input employed.
Technological change isn’t the only thing that changes labor and total factor productivity. For example, changes in input prices change the relative amounts of inputs you employ to minimize production costs. These changes in input quantities due to new input prices also change labor and total factor productivity.
Labor productivity measures output per unit of input or, typically, output per labor-hour. An increase in labor productivity is frequently associated with an improvement in technology.
Again, be careful when measuring technological change by using labor productivity, because technological change isn’t the only thing that influences labor productivity. For example, labor productivity is also affected by education, experience, motivation, and attitude of the worker.
How to calculate total factor productivity
An alternative measure of productivity is total factor productivity. Total factor productivity measures changes in output relative to changes in the quantity employed of all inputs. Use the following formula to calculate total factor productivity, represented by the symbol α:
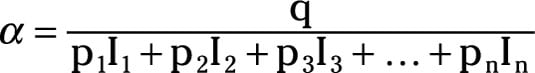
where q represents the firm’s quantity of output, I1 through In represent the quantity employed of inputs 1 through n, and p1 through pn represent the prices of inputs 1 through n.
Suppose your firm produces 100,000 units of output. In order to produce that output, the firm uses 1,200 hours of labor, 600 machine-hours of capital, and 20,000 kilowatt-hours of electricity. If input prices are $10 per hour for labor, $5 per machine-hour for capital, and $0.04 per kilowatt-hour for electricity, you can use the following steps to calculate your firm’s total factor productivity:
Substitute the quantity of output, 100,000, for q.
For each input, insert the input price for p and the input quantity for I in the bottom of the equation.
In the example, p1 is $10 and I1 is 1,200; p2 is $5 and I2 is 600; and p3 is $0.04 and I3 is 20,000.
Calculate the value in the bottom of the equation.
Divide the top of the equation by the bottom of the equation.
So, total factor productivity equals
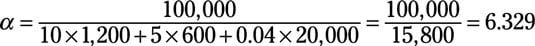
If prices are held constant over time, changes in total factor productivity represent changes in the firm’s efficiency. Increases in total factor productivity represent improvements in a firm’s efficiency that result from technological change.
Suppose five years ago, your firm produced 80,000 units of output by using 1,600 hours of labor, 500 machine-hours of capital, and 18,000 kilowatt-hours of electricity. If you hold input prices constant or the same as in the last example at $10 per hour for labor, $5 per machine-hour for capital, and $0.04 per kilowatt-hour for electricity, any change in the total factor productivity value results from changing input quantities.
Using the same steps to calculate the firm’s total factor productivity:
Substitute the quantity of output, 80,000, for q.
For each input, insert the constant input price for p multiplied by the input quantity for I in the bottom of the equation.
So, p1 is $10 and I1 is 1,600; p2 is $5 and I2 is 500; and p3 is $0.04 and I3 is 18,000.
Calculate the value in the bottom of the equation.
Divide the top of the equation by the bottom of the equation.
So, total factor productivity equals
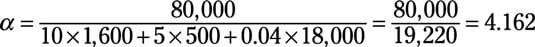
Based on the two examples, total factor productivity in the last year is 152.1 percent (6.329/4.162) of the first year’s value. Alternatively, total factor productivity increased 52.1 percent over the five-year period.

