In econometrics, you use the chi-squared distribution extensively. The chi-squared distribution is useful for comparing estimated variance values from a sample to those values based on theoretical assumptions. Therefore, it’s typically used to develop confidence intervals and hypothesis tests for population variance. First, however, you should familiarize yourself with the characteristics of a chi-squared distribution.
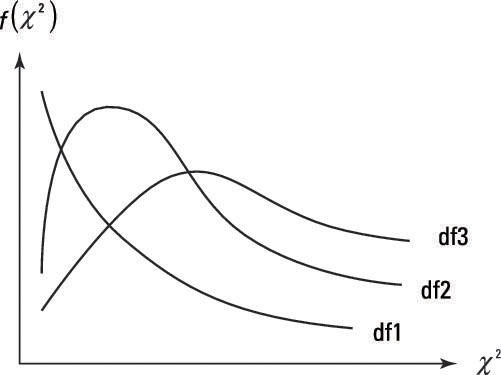
The chi-squared distribution is a squared standard normal random variable, so it takes only nonnegative values and tends to be right-skewed. The extent of its skewness depends on the degrees of freedom or number of observations. The higher the degrees of freedom (more observations), the less skewed (more symmetrical) the chi-squared distribution.
The figure shows a few chi-squared distributions, where df1, df2, and df3 indicate increasing degrees of freedom.
The chi-squared distribution is typically used with variance estimates and rests on the idea that you begin with a normally distributed random variable, such as
With sample data, you estimate the variance of this random variable with
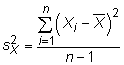
If you algebraically manipulate this formula, you arrive at the chi-squared distribution:
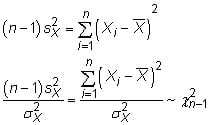
The last step, in which you divide both sides by the known (or assumed) population variance, is what standardizes your sample variance to a common scale known as chi-squared.

